| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 데이터베이스
- 프린세스메이커
- Unseen
- 마인크래프트뮤지컬
- 레베카
- 미니프로젝트
- 언리얼프로그래머
- R
- 디자드
- Jinja2
- 으
- 스터디
- 언리얼뮤지컬
- 정글사관학교
- JWT
- Enhanced Input System
- 게임개발
- Ajax
- 카렌
- EnhancedInput
- 알고풀자
- 파이썬서버
- 프메
- Express
- 스마일게이트
- flask
- VUE
- Bootstrap4
- node
- 언리얼
- Today
- Total
Today, I will
Sentinel node를 사용하여 구현한 레드블랙 트리(2) - 삭제로직 본문
1. 레드블랙트리 삭제로직 살펴보기
안녕하세요! FlyDuck Dev🦢입니다. 지난 포스팅에 이어서 레드블랙트리 삭제로직을 살펴보도록 하겠습니다.
참고 영상: https://youtu.be/lU99loSvD8s
2. 삭제로직

레드 블랙 트리에서 삭제연산을 진행할 때 크게 고려할 세가지 케이스는
-1- 왼쪽 차일드노드가 NIL일때,
-2- 오른쪽 차일드노드가 NIL일때,
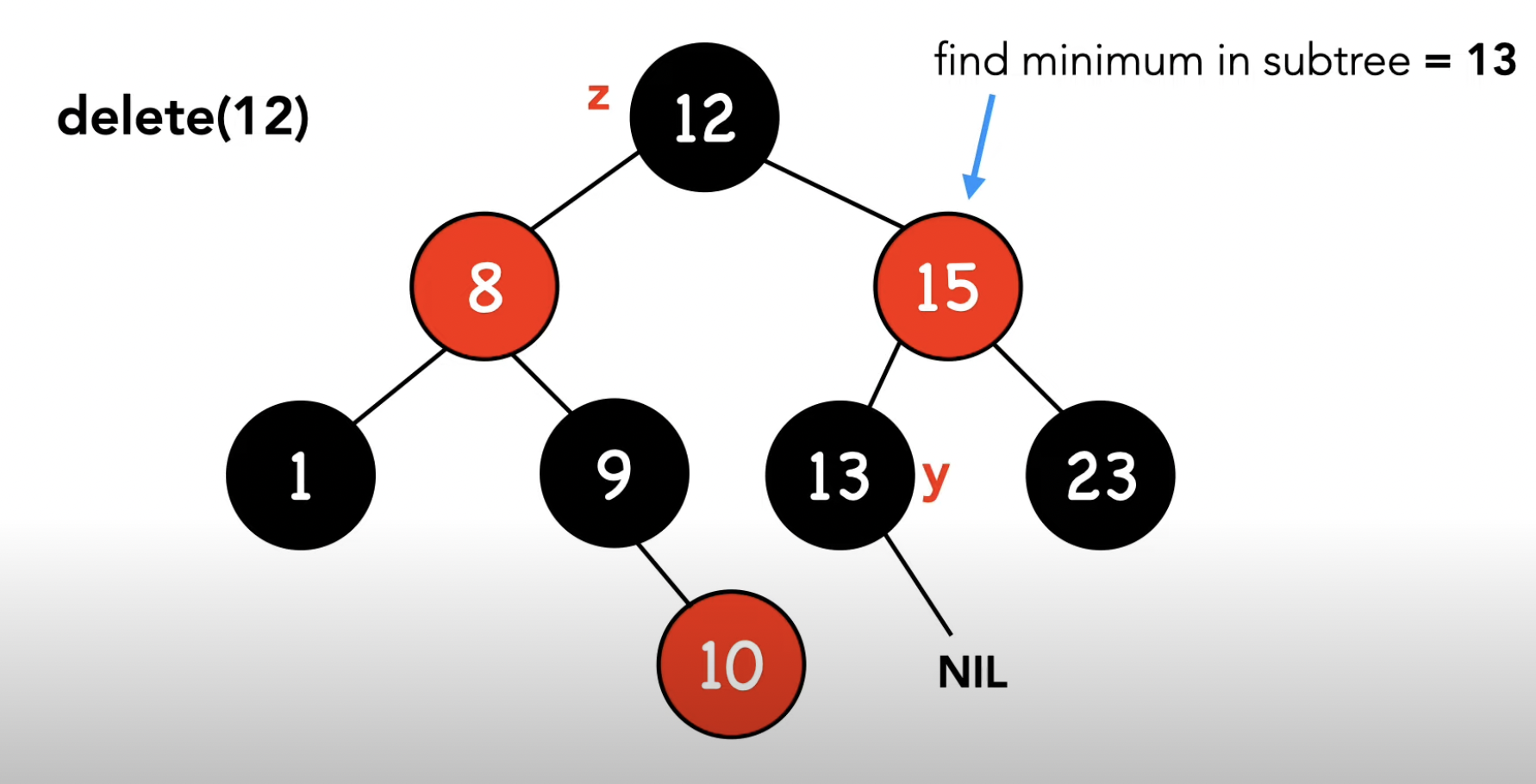
-3- 양쪽 차일드노드가 모두 NIL이 아닐 때, 입니다.
-1- 왼쪽 차일드노드가 NIL
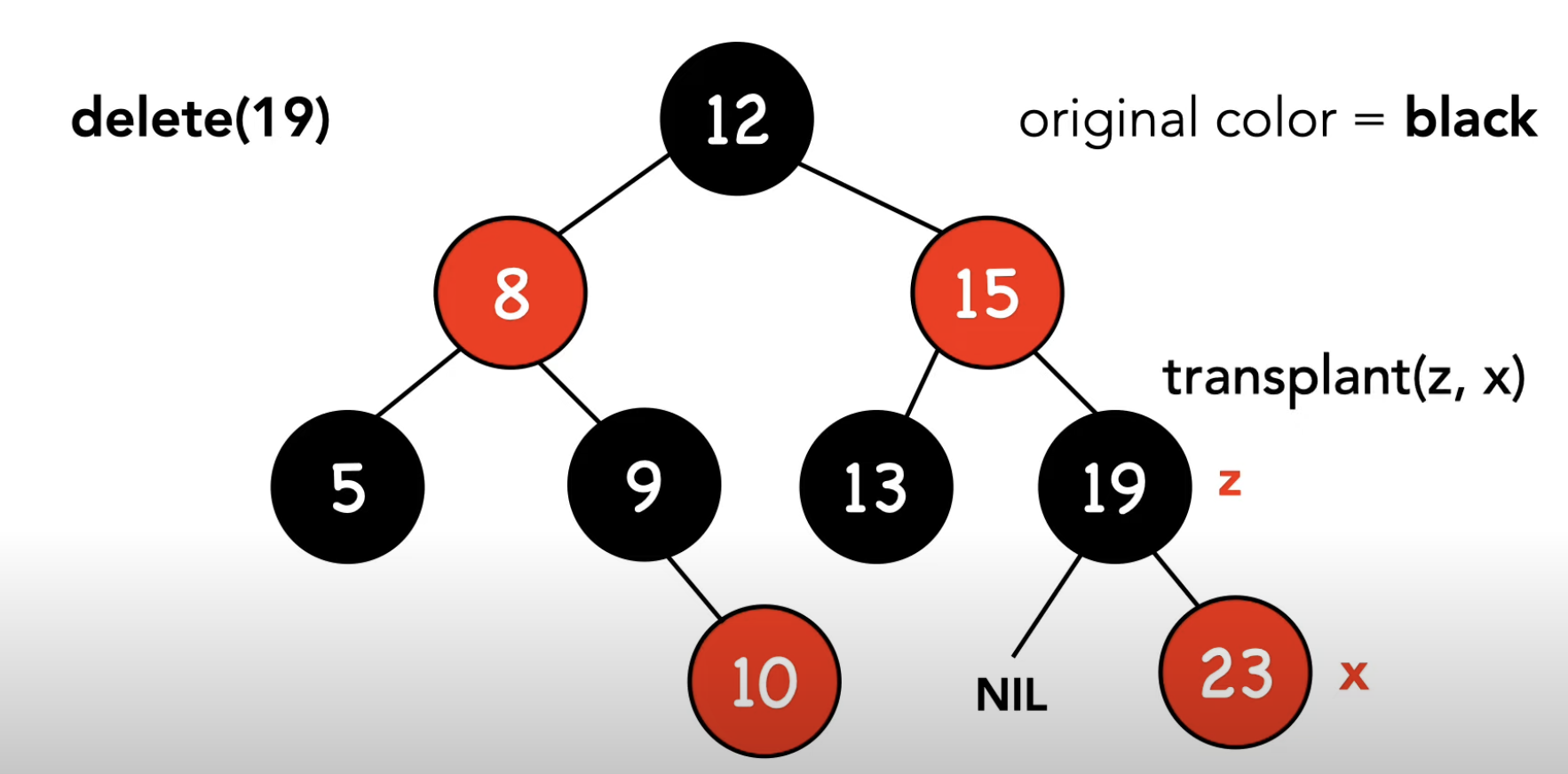
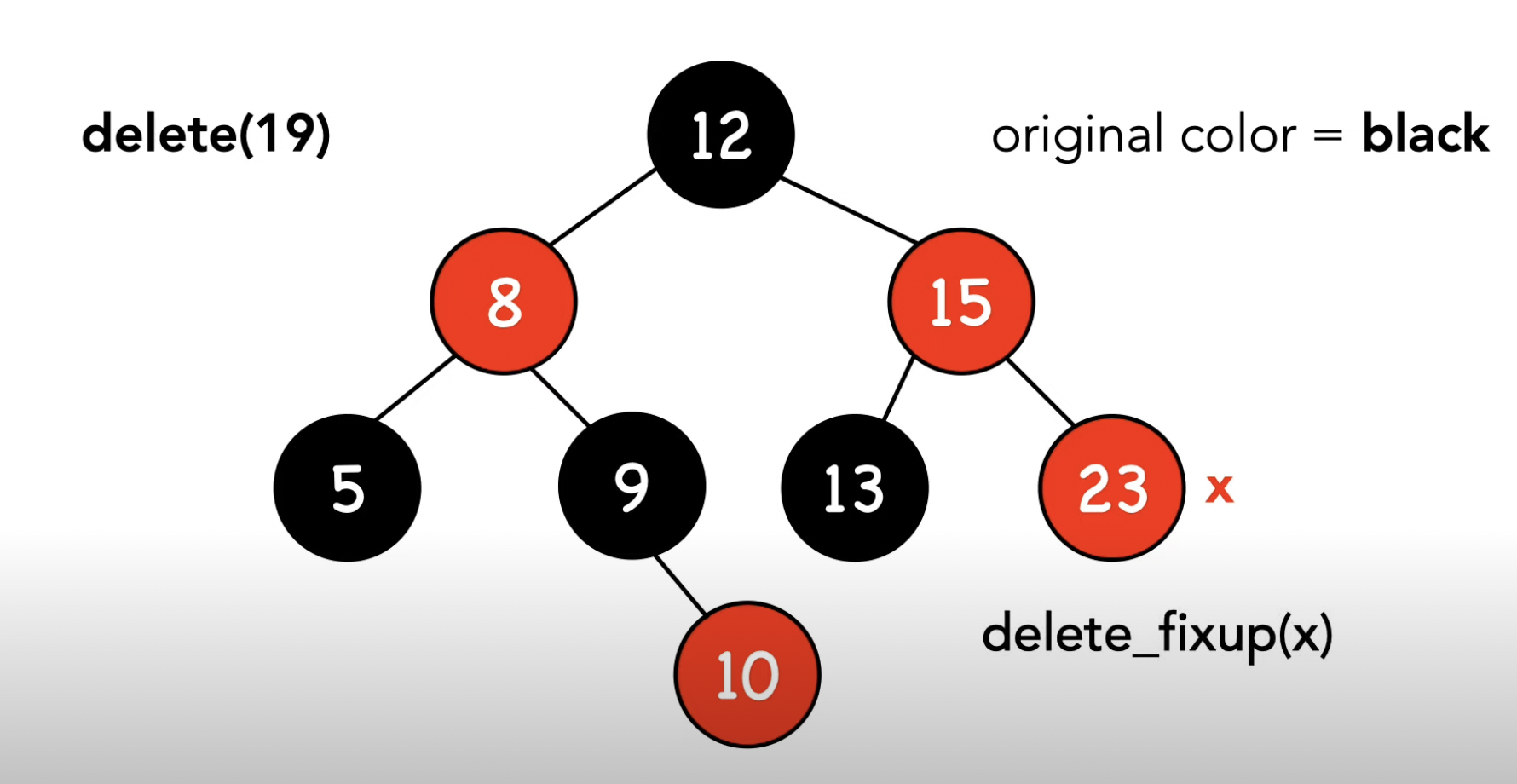
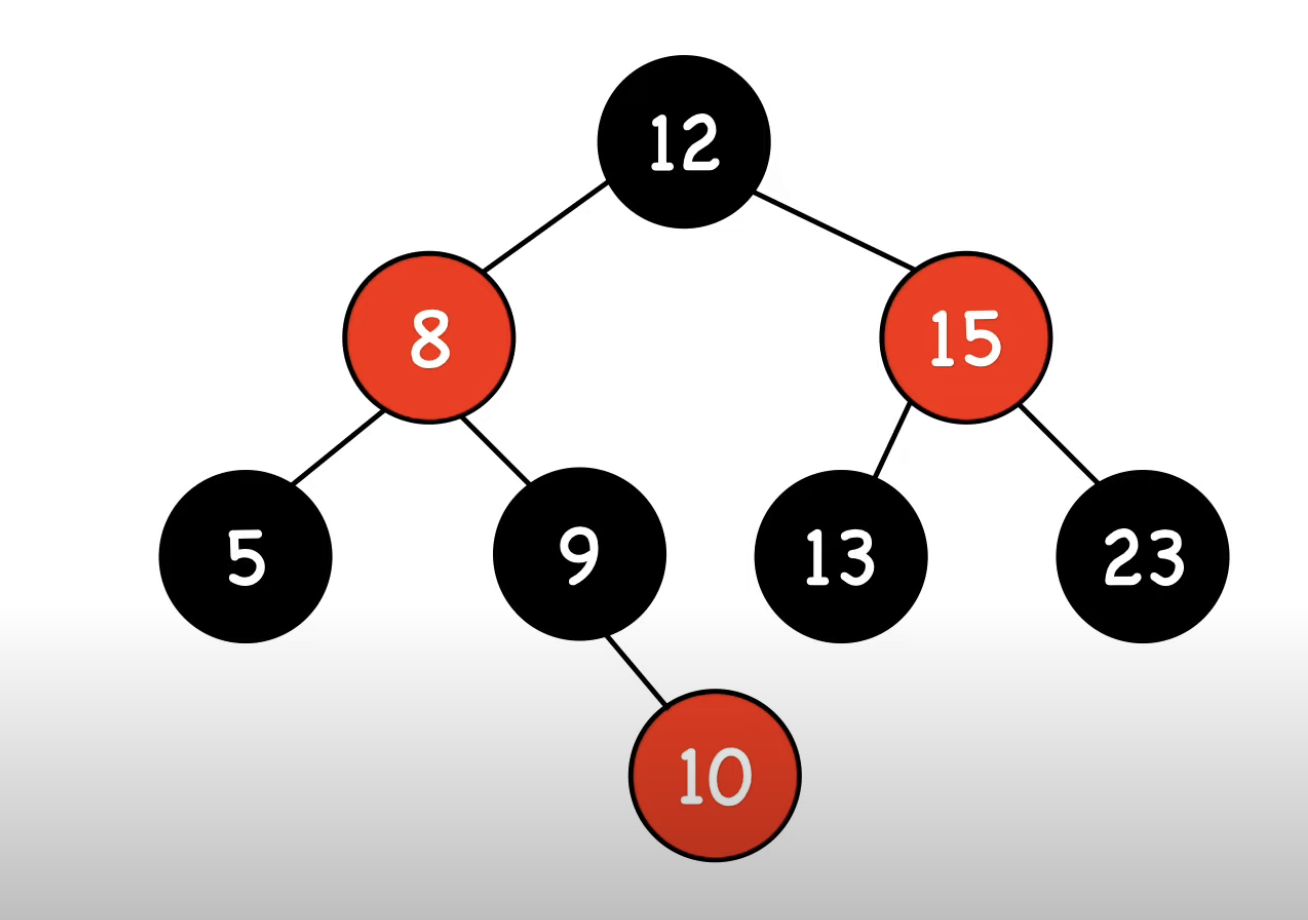
-2- 오른쪽 차일드노드가 NIL
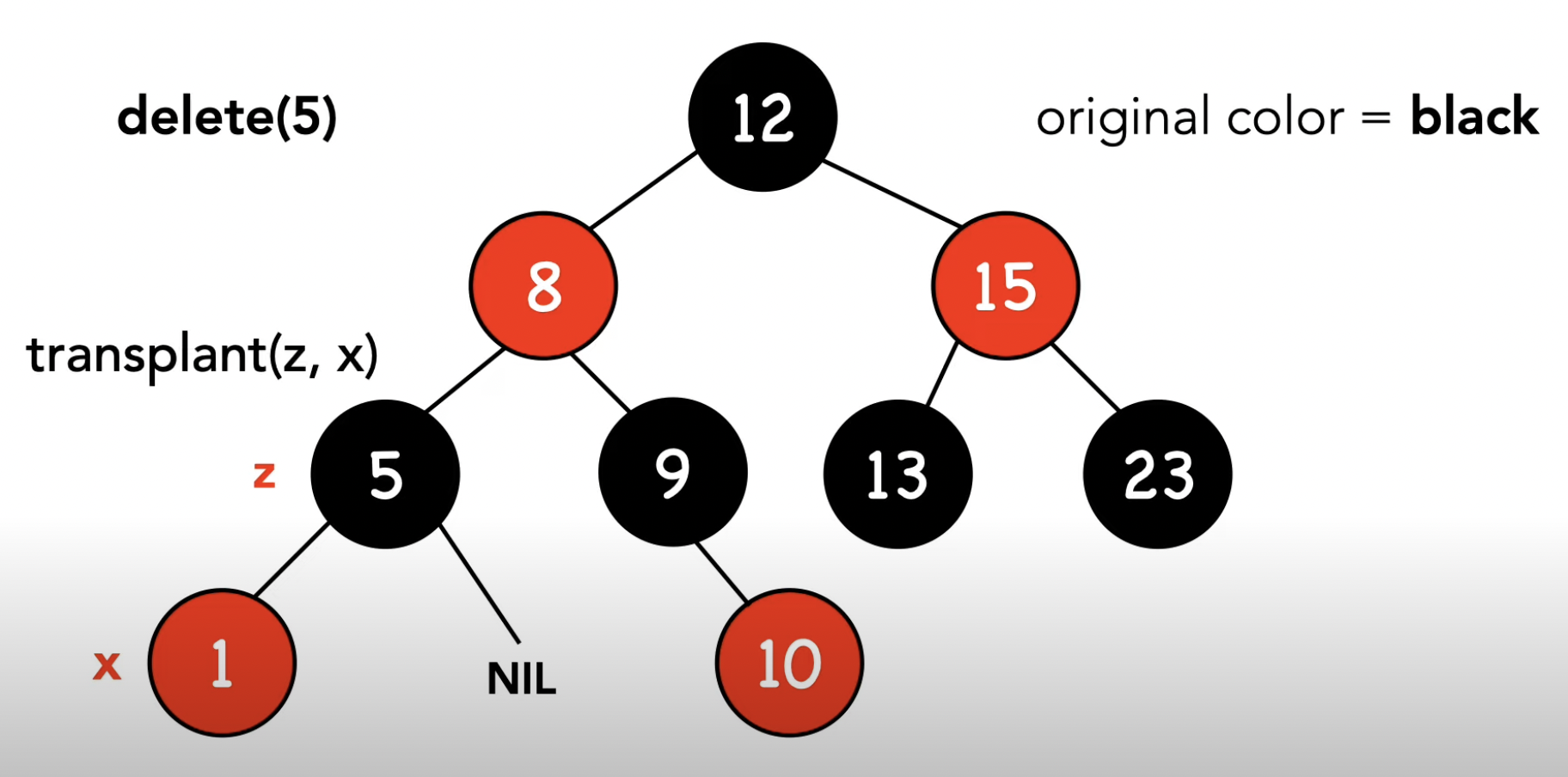
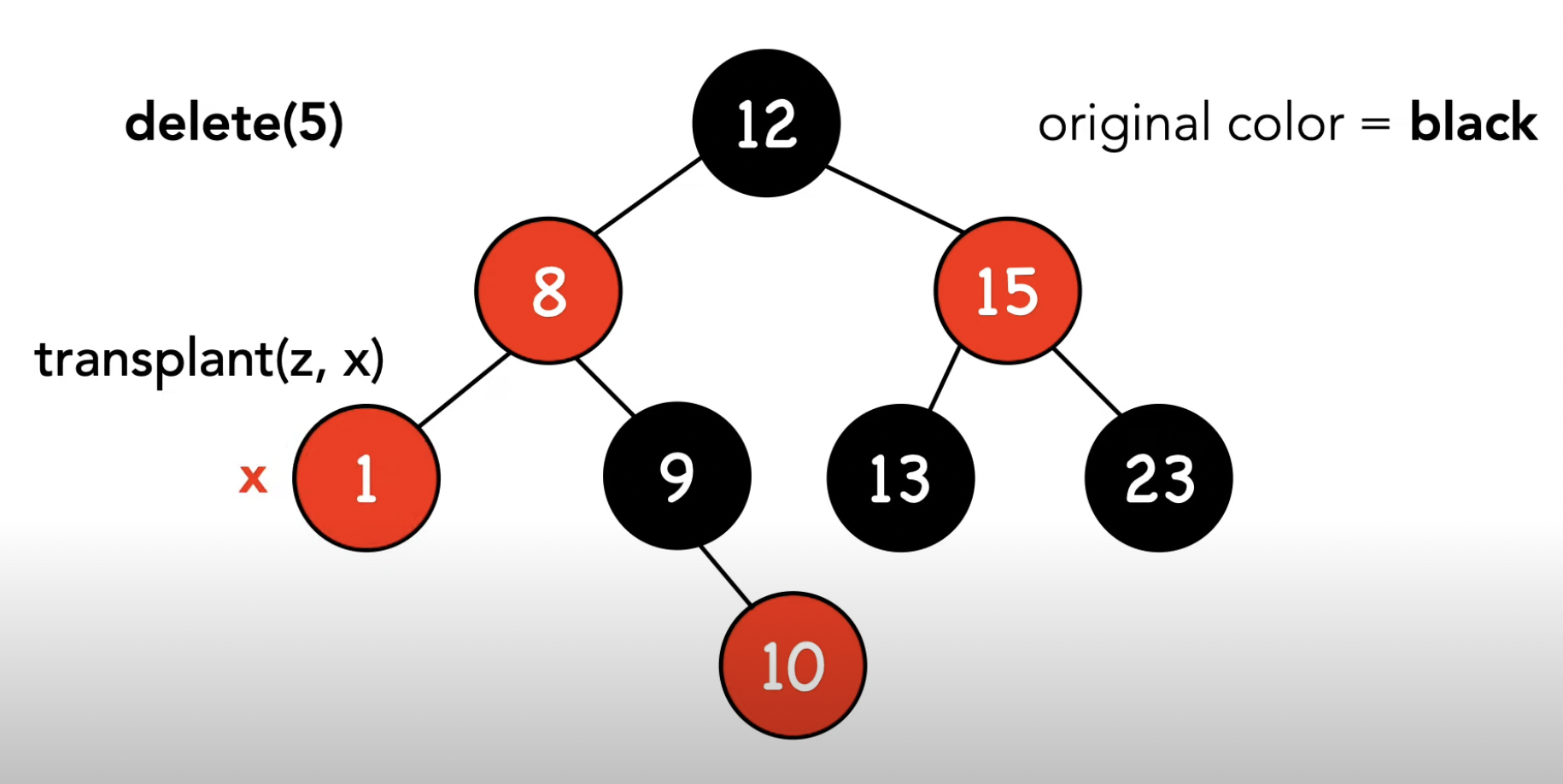
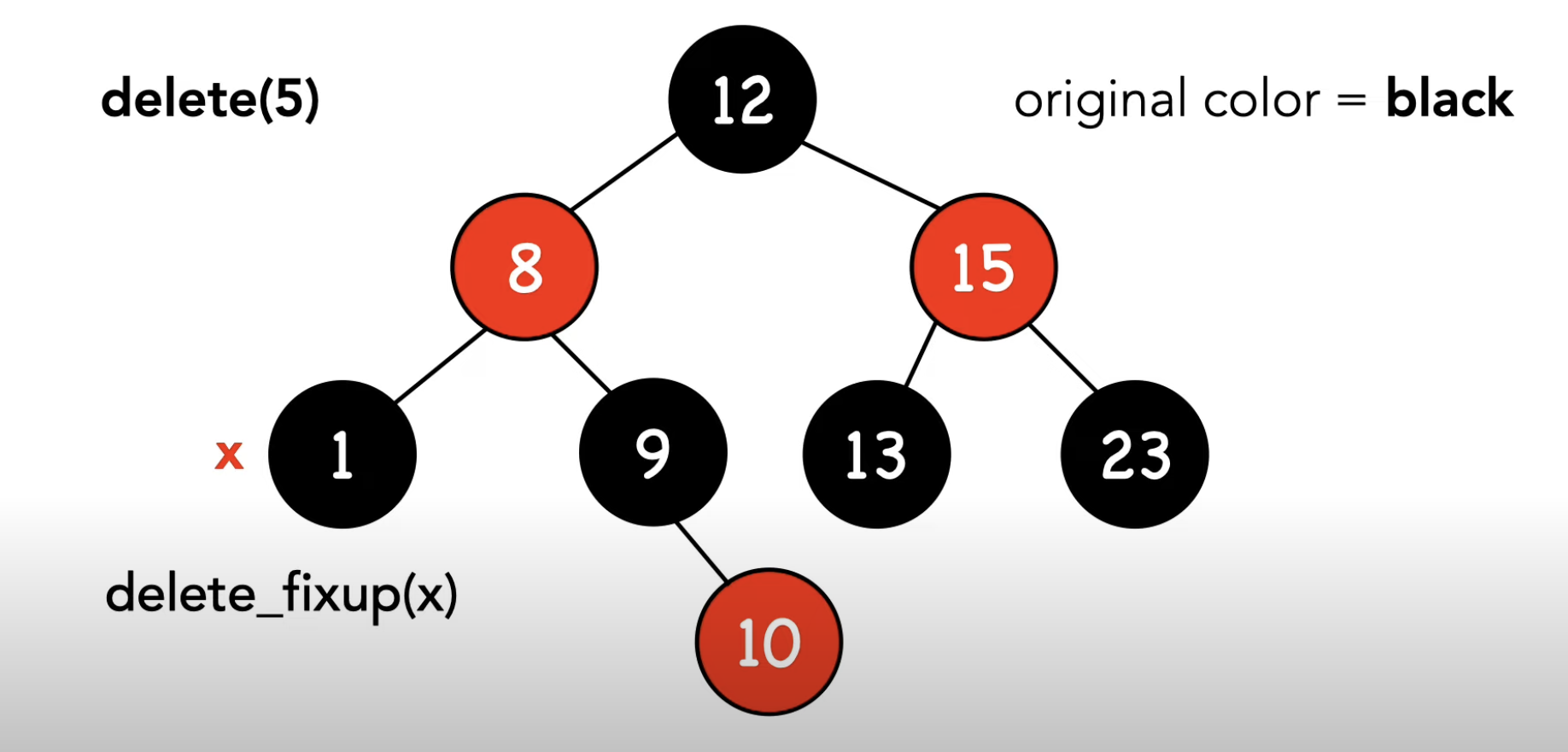
-3- 양쪽 차일드노드가 모두 NIL이 아님
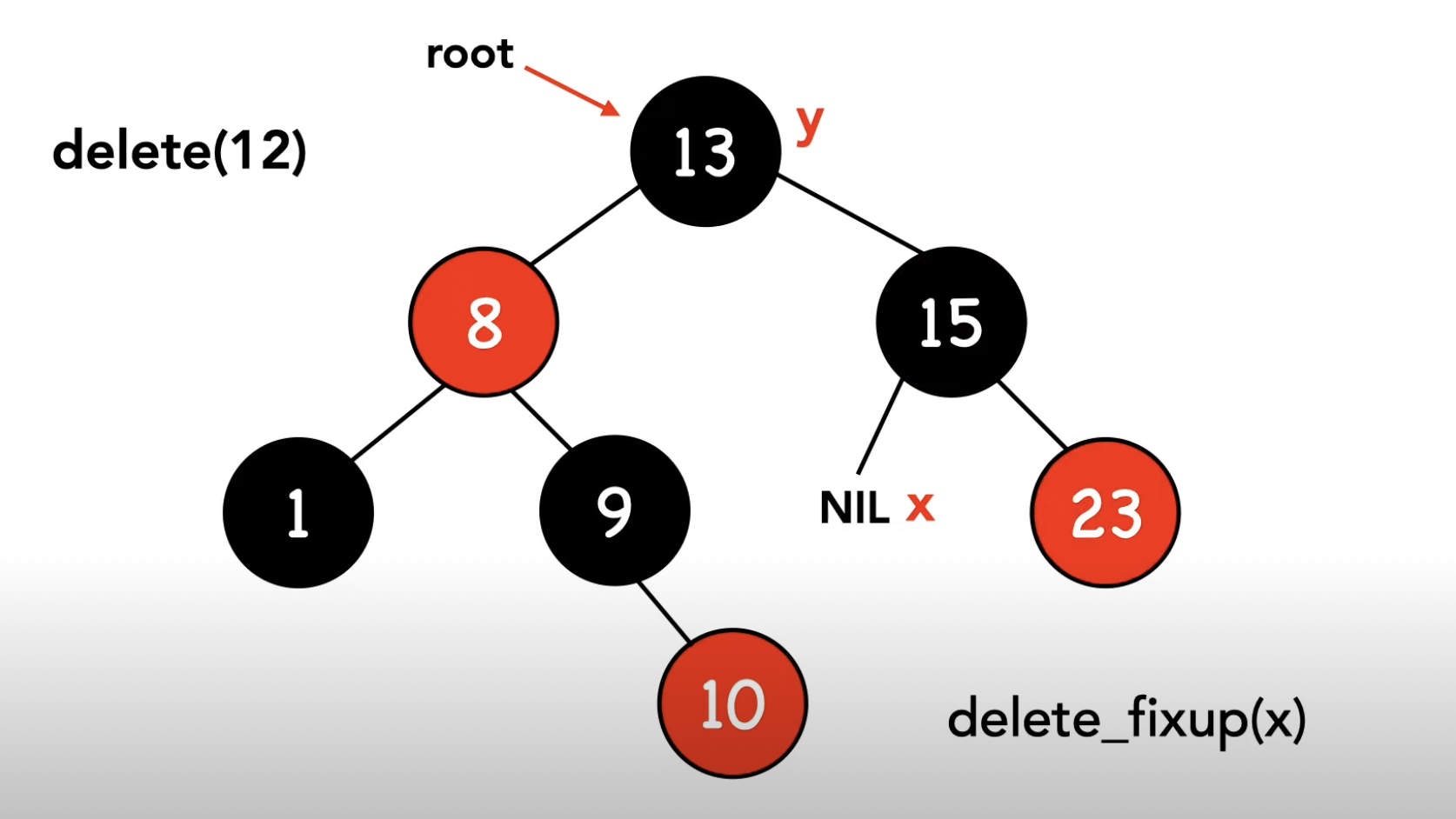
(1) rbtree_erase
수도코드와 c코드를 살펴보겠습니다.

int rbtree_erase(rbtree *t, node_t *z) {
node_t *y = z;
color_t y_original_color = y->color;
node_t *x; // x는 y의 자식이자 오른쪽 서브트리에서 가장 작은 값을 가진 노드
if (z->left == t->nil) { // -1- 왼쪽 차일드노드가 NIL
x = z->right;
rbtree_transplant(t, z, z->right);
} else if (z->right == t->nil) { //-2- 오른쪽 차일드노드가 NIL
x = z->left;
rbtree_transplant(t, z, z->left);
} else { // -3- 양쪽 차일드노드가 모두 NIL이 아님
y = find_min_successor(t, z->right); // z의 오른쪽 서브 트리에서 successor를 찾는다.
// z보다 크지만 오른쪽 서브 트리에서 가장 작은, z 바로 다음으로 큰 successor를 찾는 것
y_original_color = y->color;
x = y->right; // y의 자리에 x가 대체자로 올라옴
if (y->parent == z) {
x->parent = y;
} else {
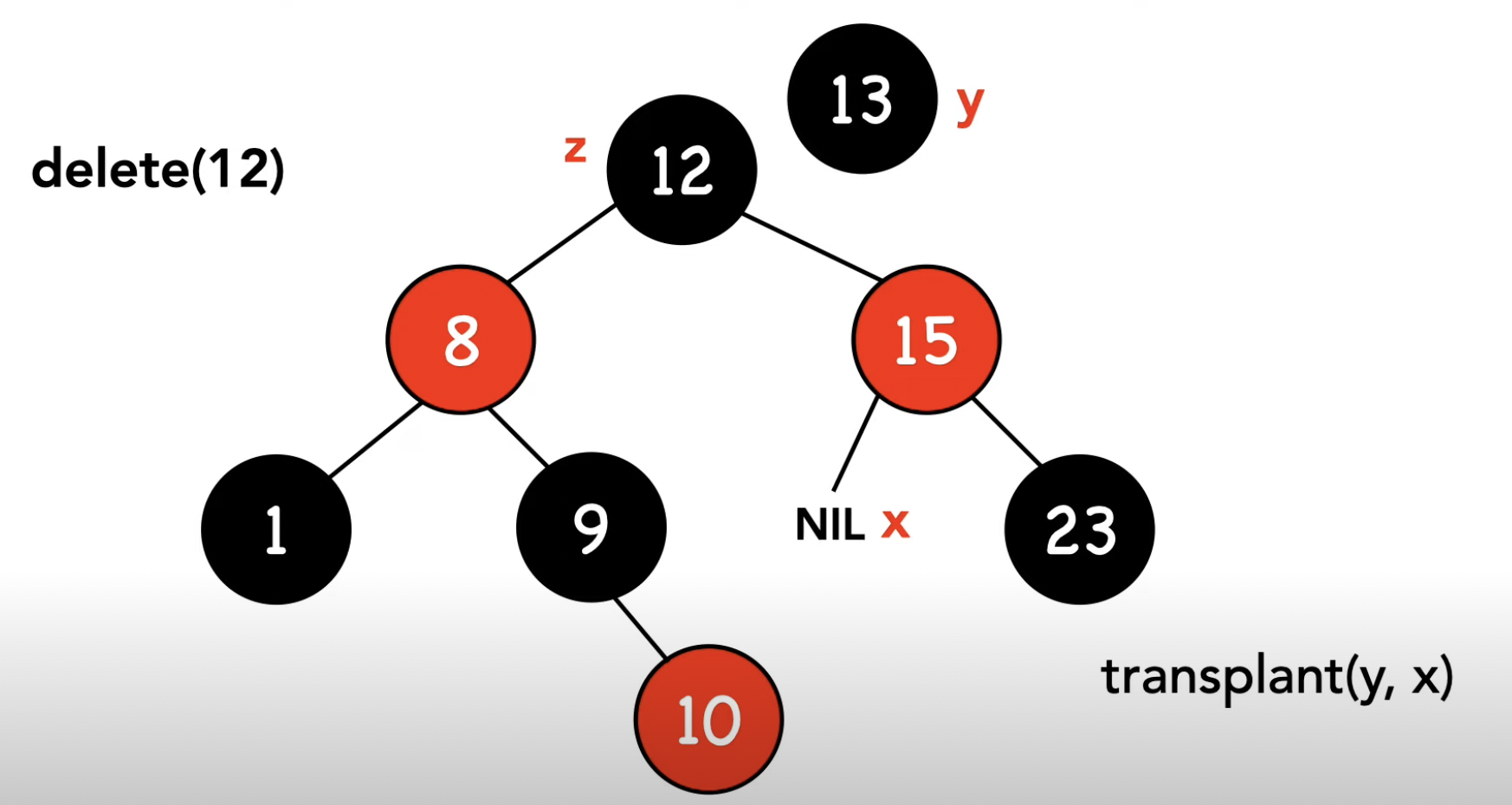
rbtree_transplant(t, y, y->right); // z에 y를 심기 전에, 먼저 y의 자리에 y의 자식을 심는다.
y->right = z->right;
y->right->parent = y;
}
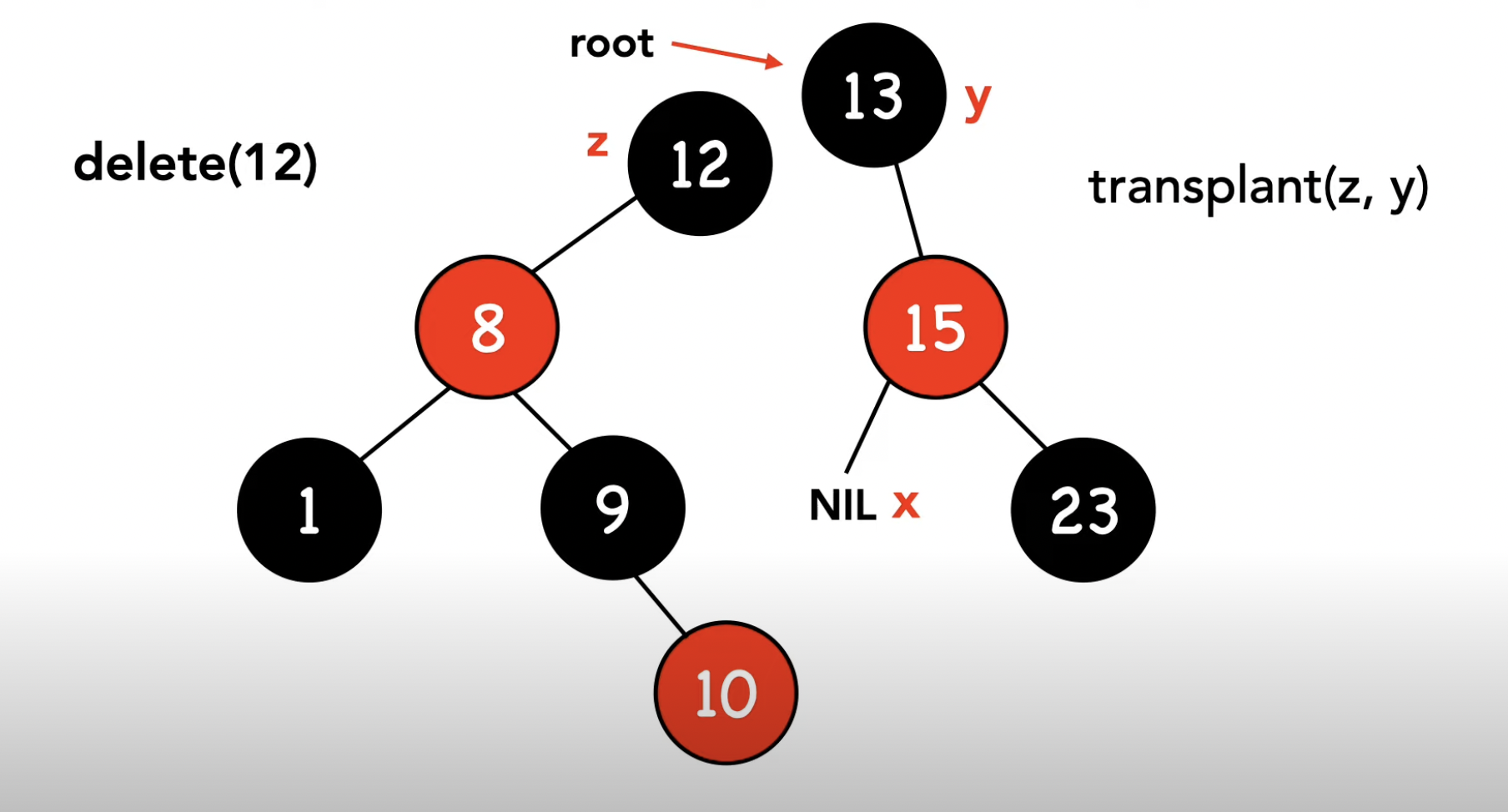
rbtree_transplant(t, z, y); // z의 부모는 이제 z가 아니라 y를 가르키게 된다.
y->left = z->left;
y->left->parent = y;
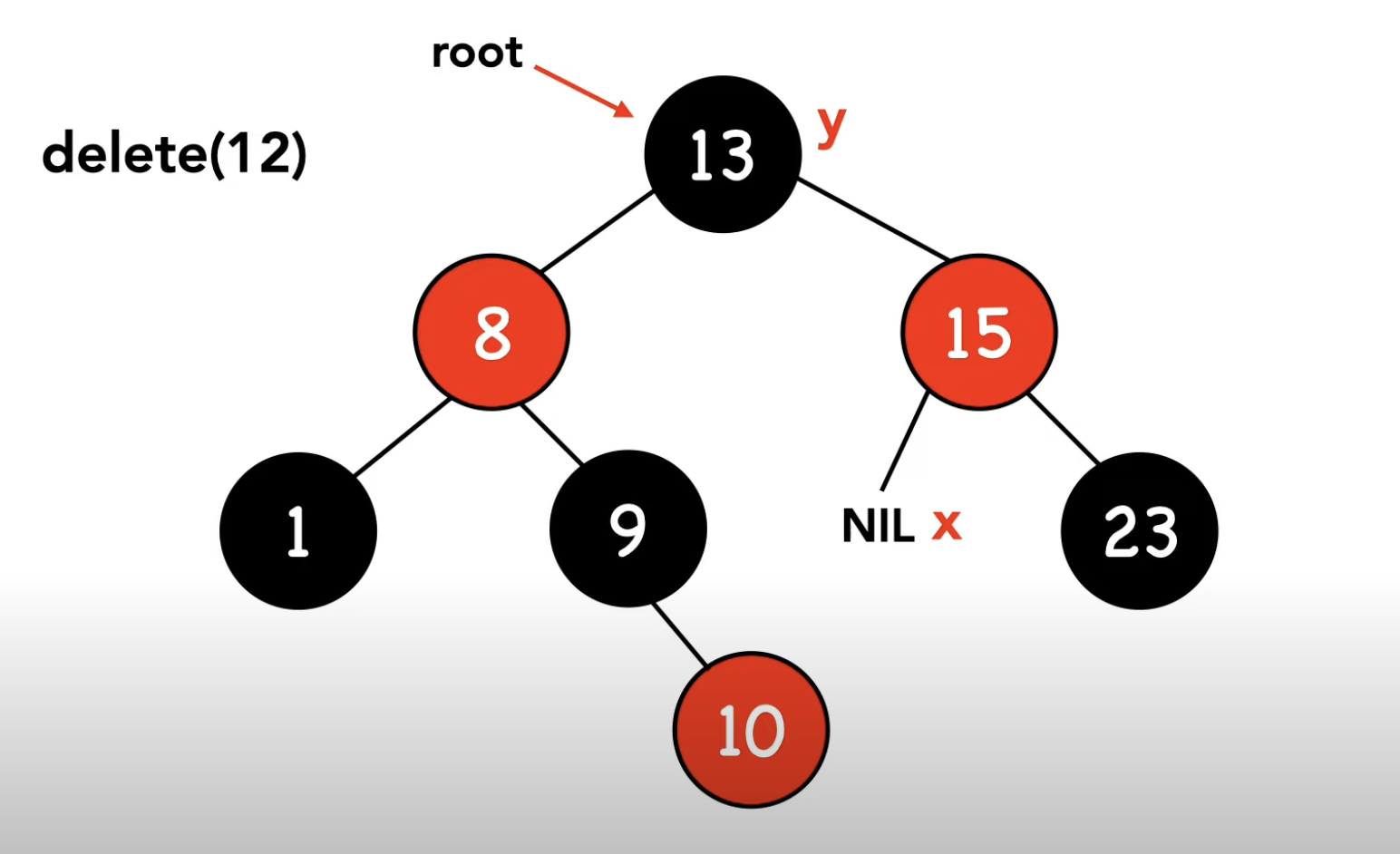
y->color = z->color; // y의 색깔만 바뀐다. z에 y가 이식된 후, z의 색깔을 y에 덧칠
}
// 실제로 삭제되는 노드인 y의 색이 red였다면 레드 블랙 트리 특성 5가지 중에서 위반되는 것은 없다.
// black이었다면 위반하는 항목들이 있기 때문에 재조정이 필요하다
if (y_original_color == RBTREE_BLACK) {
rbtree_erase_fixup(t, x);
}
free(z); // z가 삭제되고 그 자리에 y가 대체하는 것이므로 z를 free
return 0;
}(2) find_min_successor
레드블랙트리에서 노드를 삭제할 때, 해당 노드의 후계자(successor)를 찾는 과정이 필요합니다. 후계자란 삭제할 노드의 다음으로 큰 값을 가진 노드를 의미합니다.
find_min_successor 함수는 삭제할 노드의 오른쪽 서브트리에서 가장 작은 값을 가지는 노드를 찾아 반환합니다.
node_t *find_min_successor(rbtree *t, node_t *y) {
while (y->left != t->nil) { // y의 왼쪽 자식이 nil이 아닐 때까지 계속 파고들어간다.
y = y->left;
}
// y의 왼쪽 자식이 nil이라면 멈추기 때문에(y가 nil이면 멈추는게 아니라) y는 유의미한 값을 가진 노드를 가르키는 주소값이다. successor.
return y;
}이 함수는 레드블랙트리에서 삭제 연산을 구현하는 데 중요한 역할을 합니다. 삭제할 노드의 후계자를 찾은 후에는 해당 노드의 값을 후계자의 값으로 대체하고, 후계자 노드를 삭제합니다. 이렇게 하면 레드블랙트리의 균형 상태를 유지하면서 노드를 삭제할 수 있습니다.
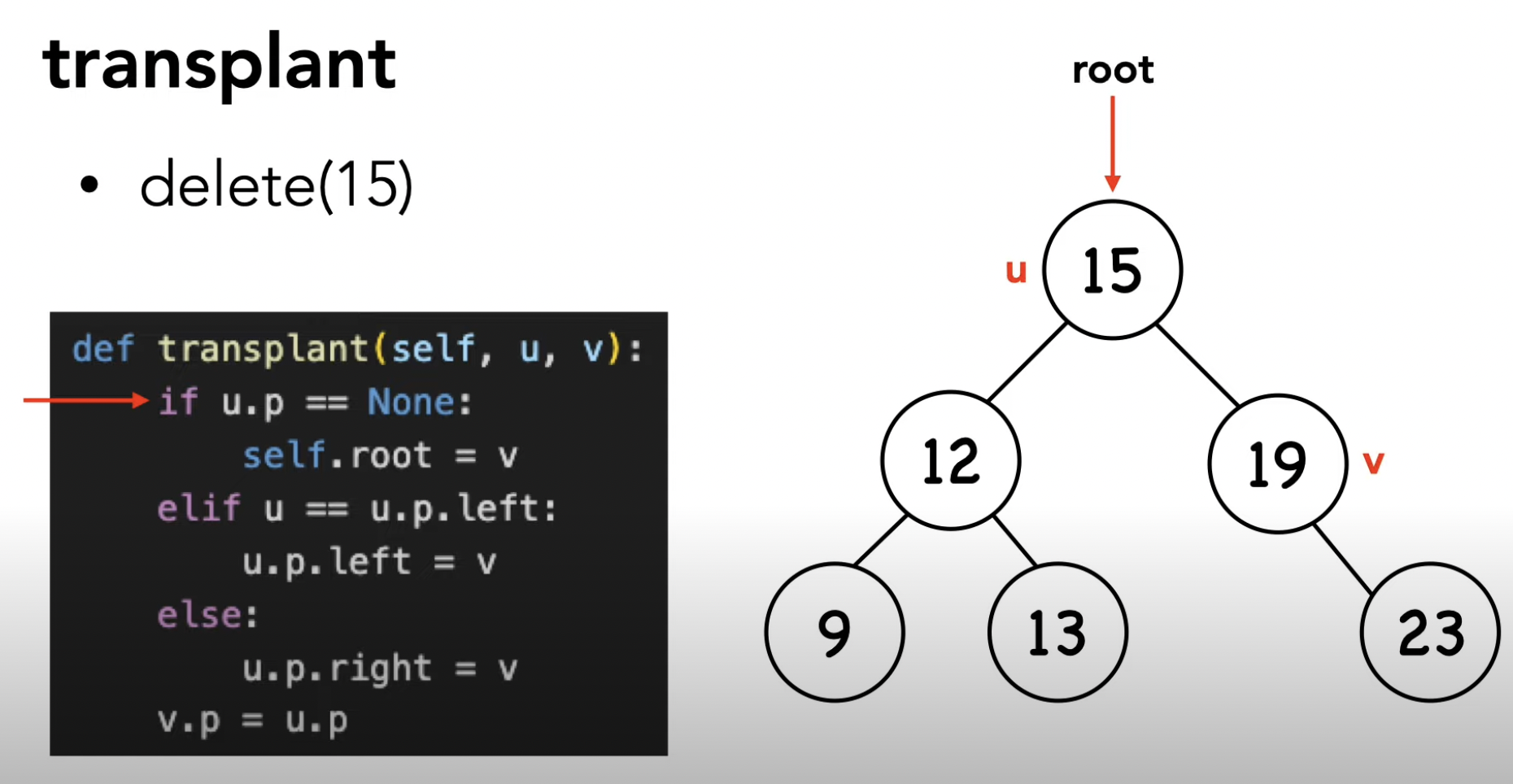
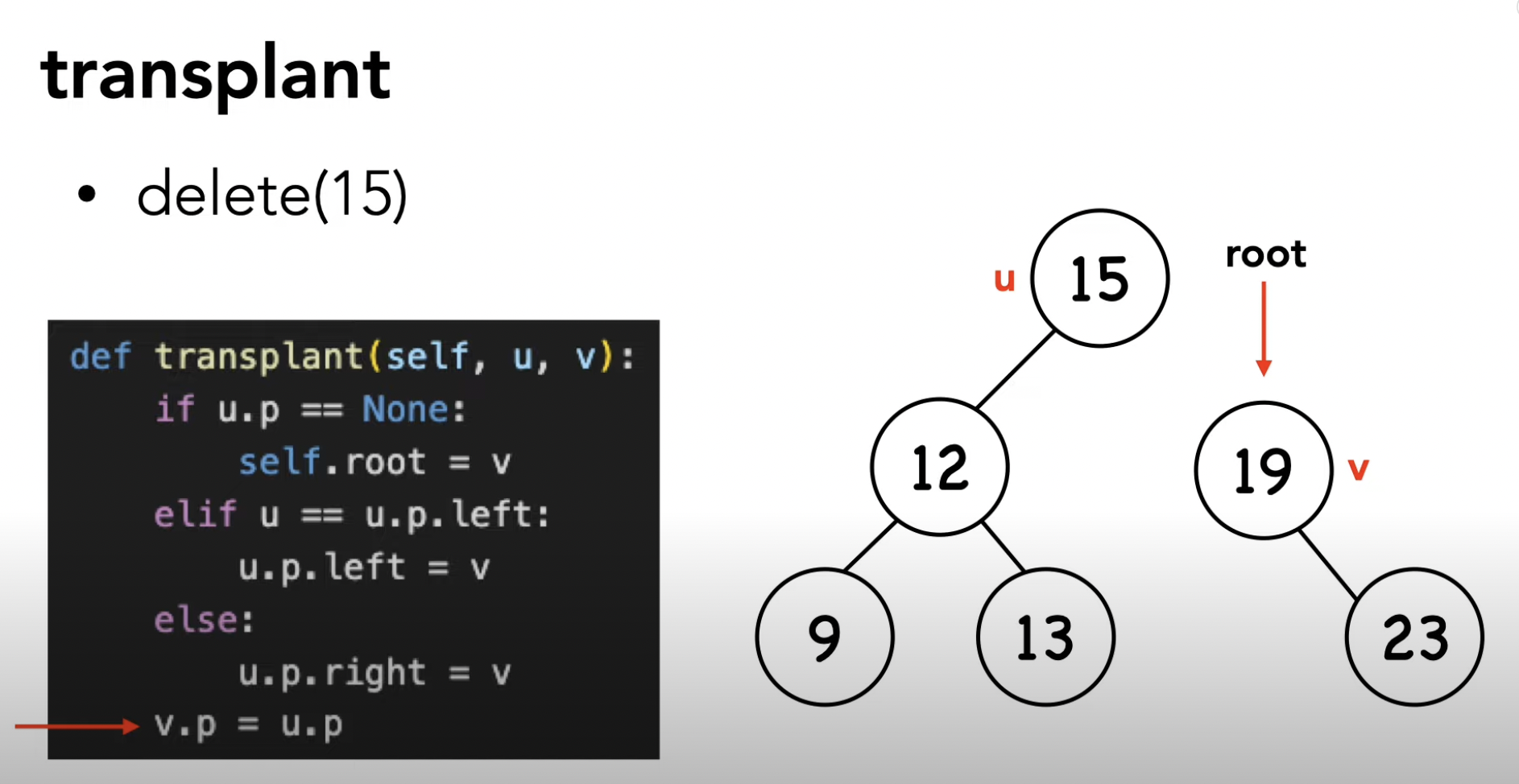
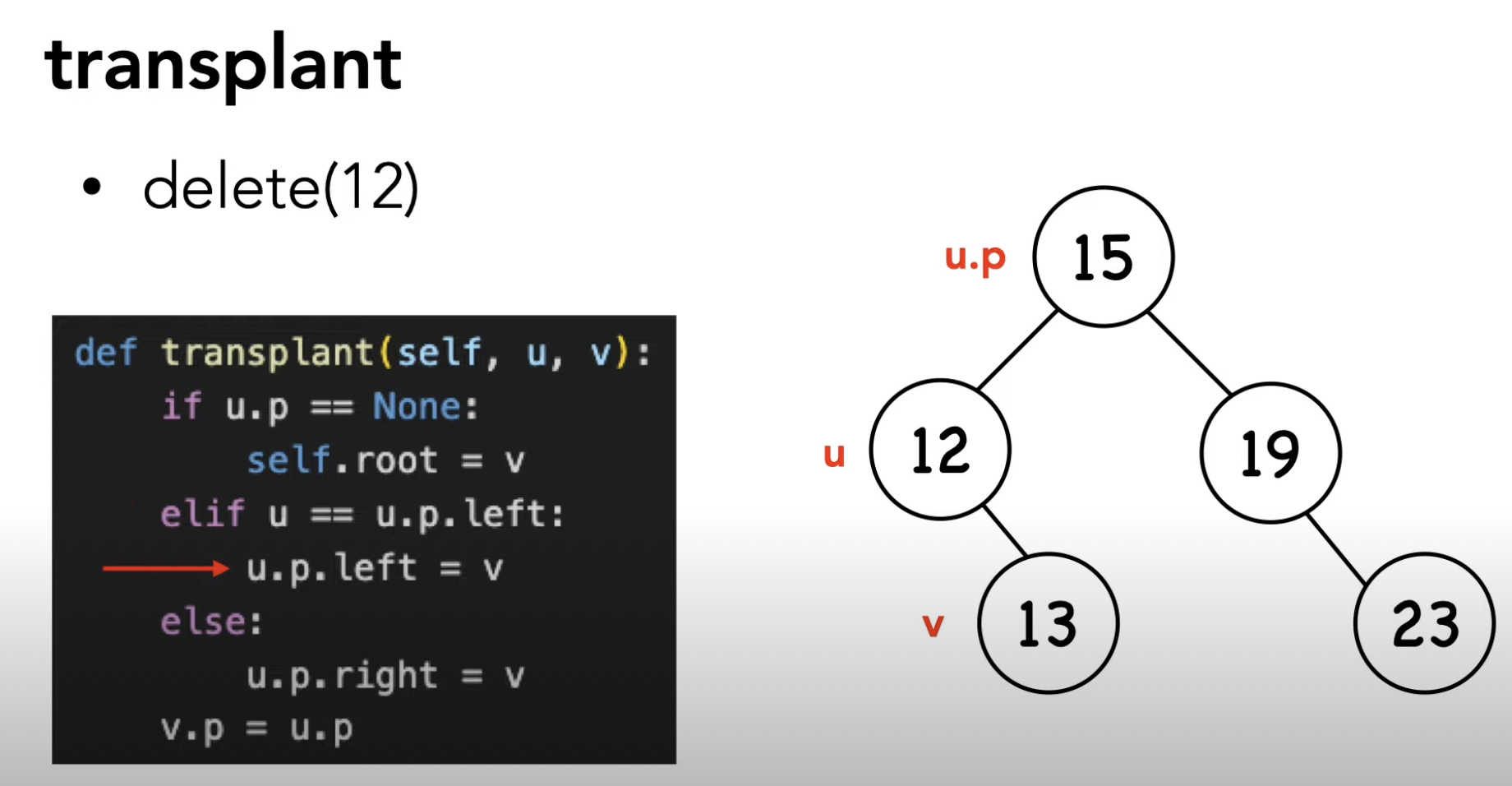
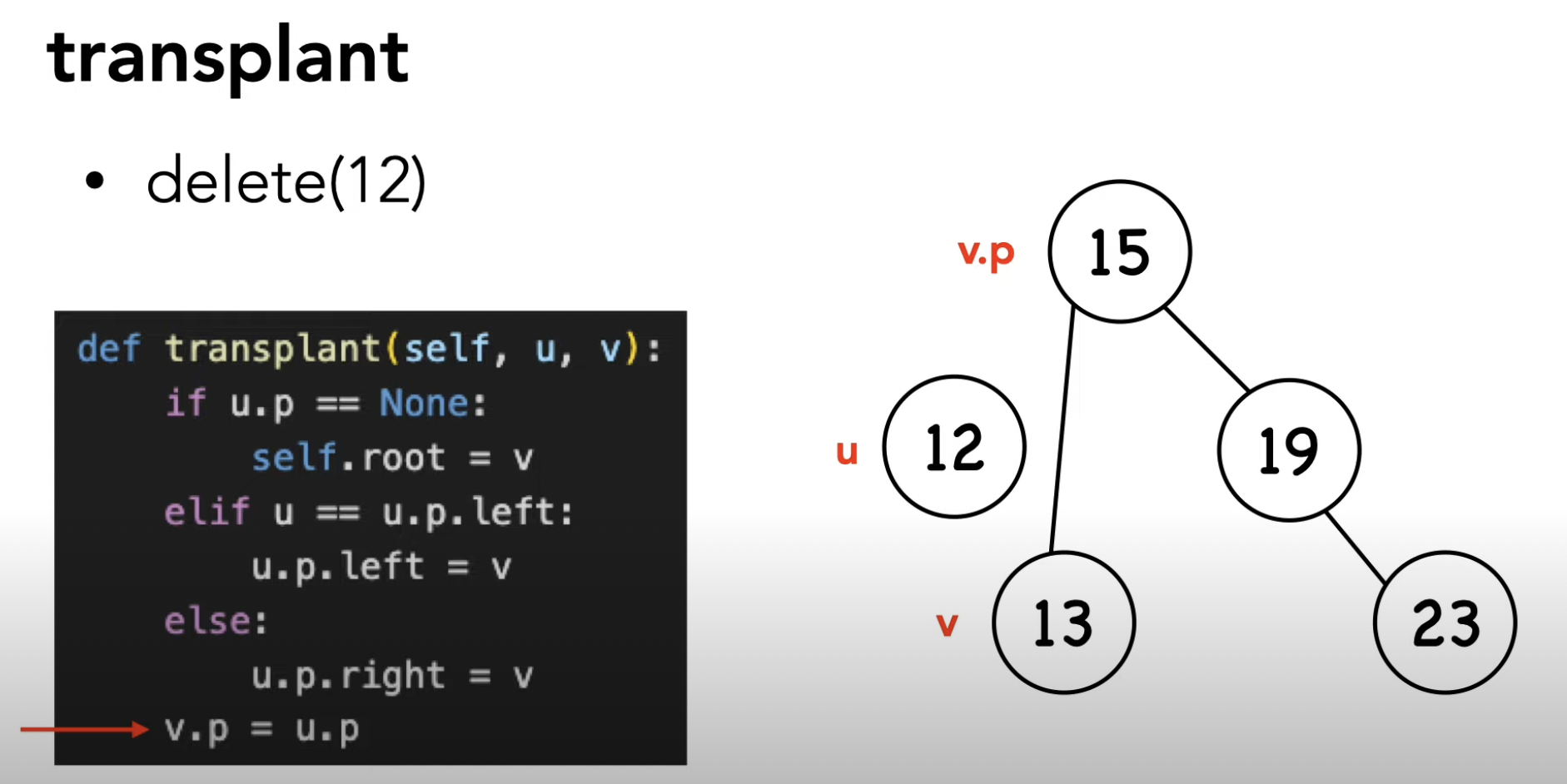
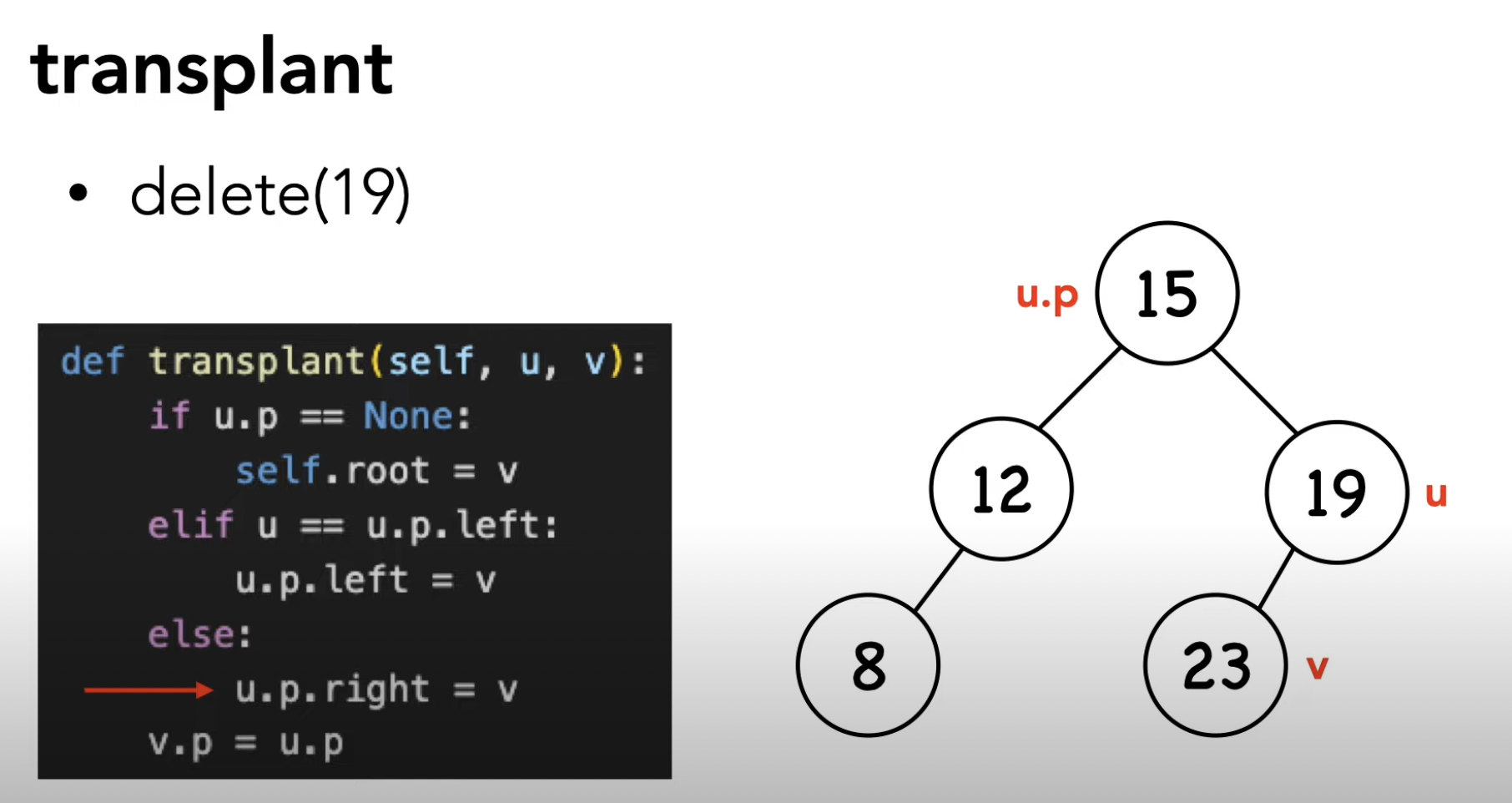
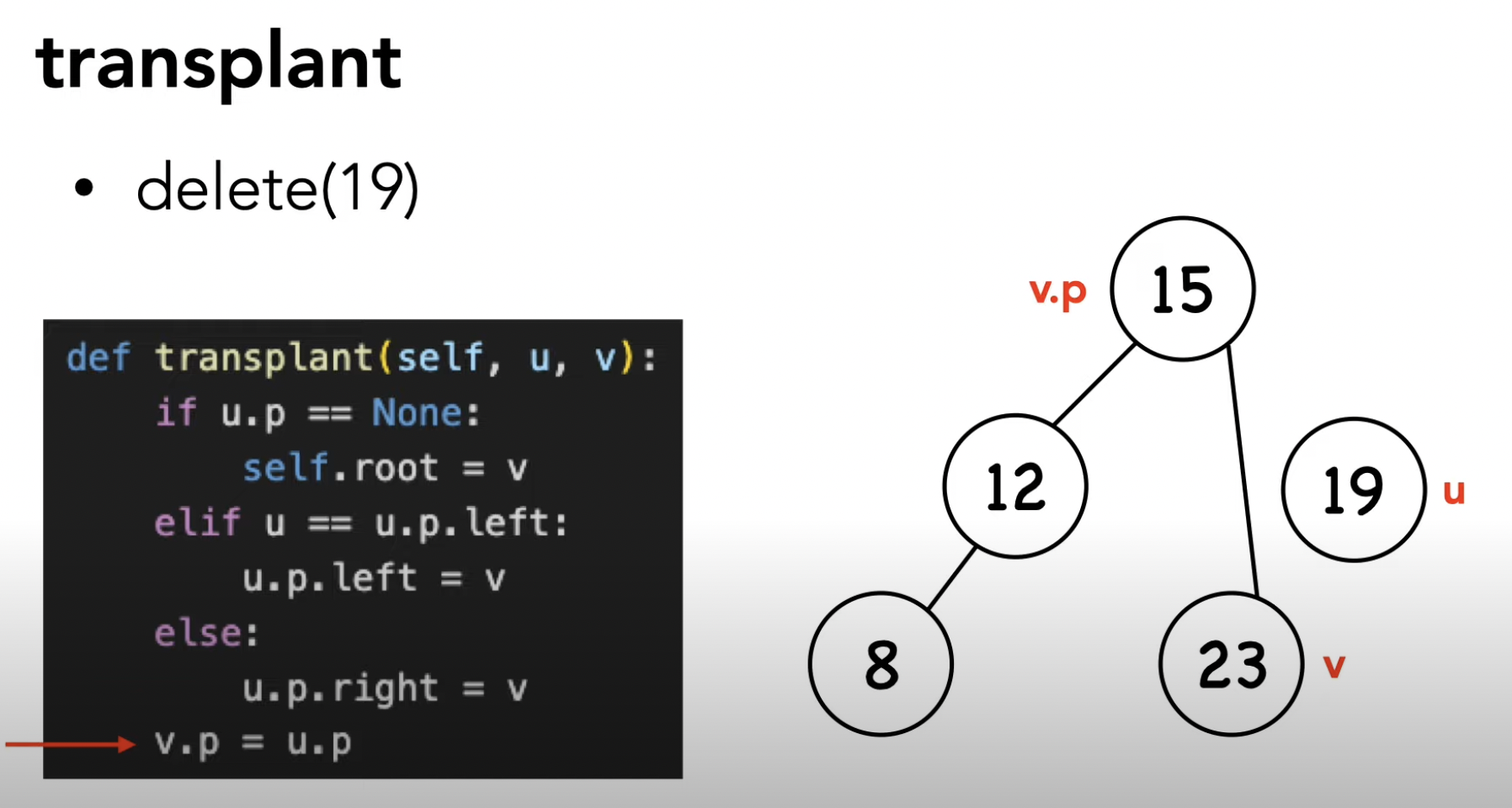
(3) rbtree_transplant

레드블랙 트리에서 노드를 이동시키는 함수로,
삭제 연산 중 삭제될 노드를 대체할 노드를 선택하고 이를 이동시켜 균형을 유지하는 역할을 합니다.
삭제될 노드와 대체될 노드의 부모 및 자식 관계를 조정하여 레드-블랙 트리의 균형을 유지합니다.
//노드 u가 노드 v로 대체되어 트리의 구조를 유지
//삭제된 노드를 대체할 노드를 선택하여 트리의 균형을 유지
void rbtree_transplant(rbtree *t, node_t *u, node_t *v) { // 노드 u를 노드 v로 대체
if (u->parent == t->nil) { //노드 u의 부모 노드가 nil(즉, u가 루트 노드인 경우)인지 확인
t->root = v; //루트 노드를 v로 대체
} else if (u == u->parent->left) { //u가 부모 노드의 왼쪽 자식인지 확인
u->parent->left = v; //부모 노드의 왼쪽 자식을 v로 대체
} else { //그렇지 않다면
u->parent->right = v; //부모 노드의 오른쪽 자식을 v로 대체
}
v->parent = u->parent; //v의 부모를 u의 부모로 설정
}
(4) rbtree_erase_fixup
rbtree_erase_fixup 함수는 Red-Black Tree에서 노드를 삭제한 후에 발생하는 위반된 Red-Black Tree 특성을 복구하기 위해 필요한 함수입니다.
삭제된 노드의 자리를 대신할 새로운 노드를 선택하고 이 노드의 색상이 빨간색일 경우 검은색으로 바꿔주는 등의 조치를 취하며, 이로 인해 위반된 특성을 해결하는 과정을 거칩니다. 이 함수는 이러한 과정을 반복하면서 위반된 특성을 복구해 나가는 역할을 합니다.
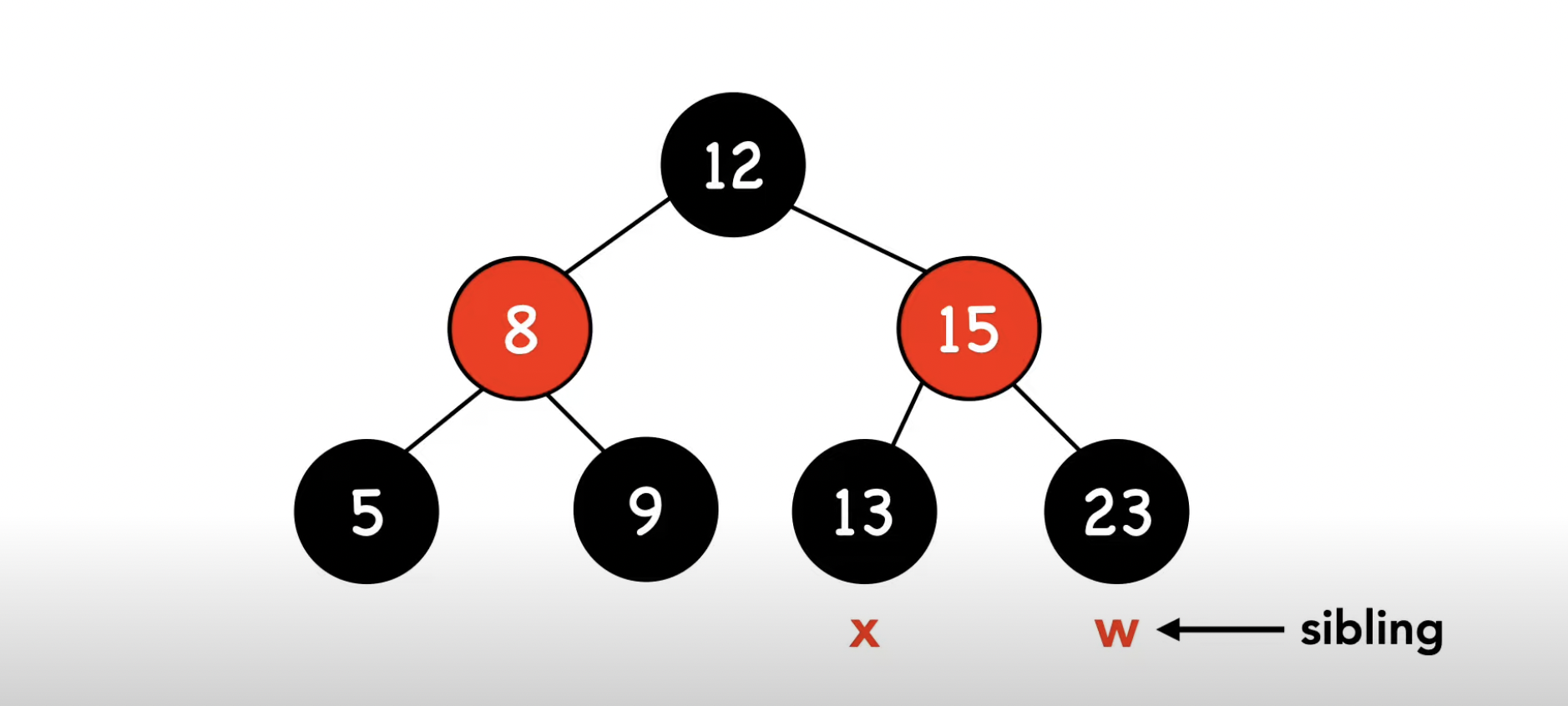
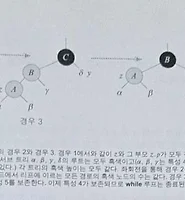
x의 형제노드가 w일때, 만날 수 있는 수정 사항은 다음 4가지입니다.
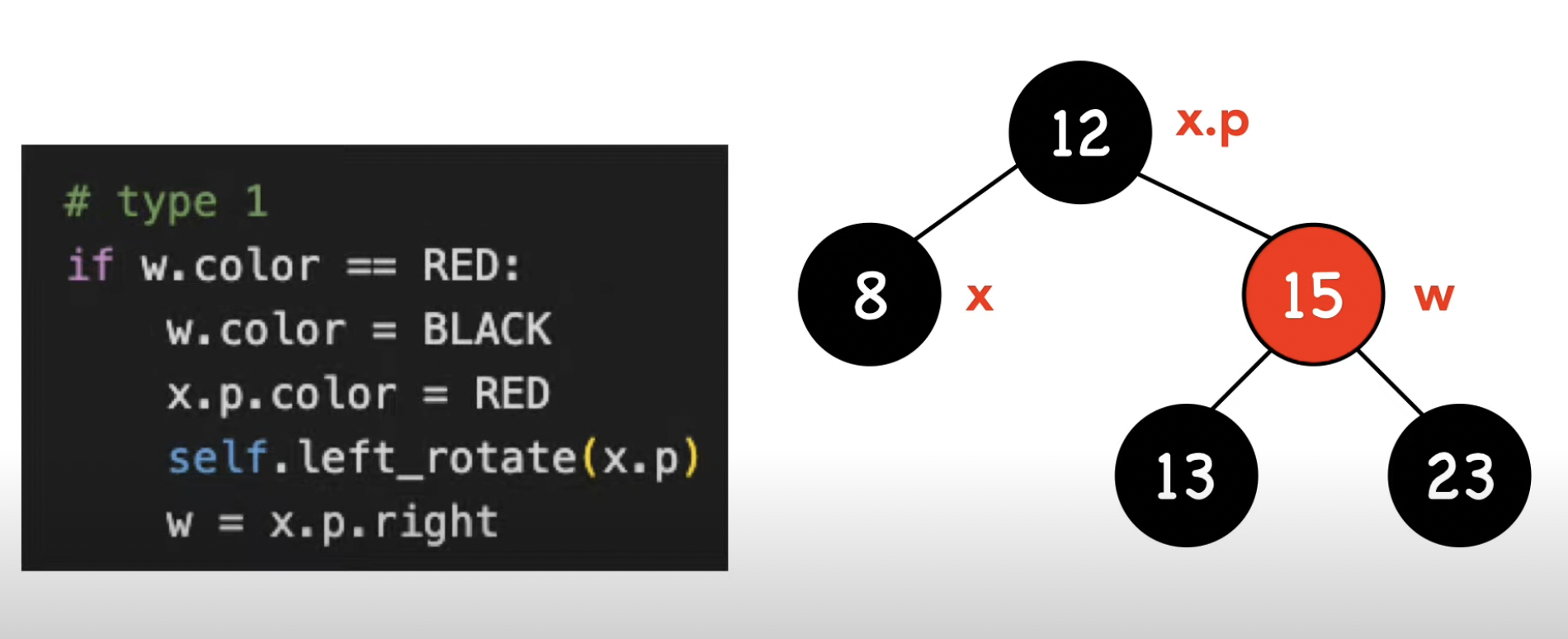
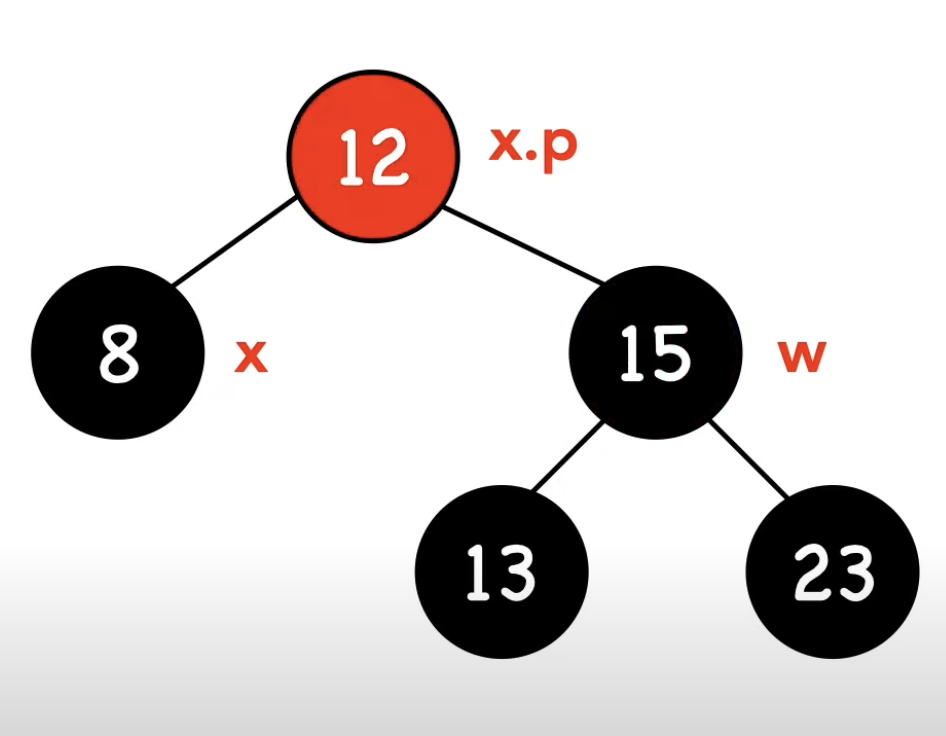
-1- w가 빨간 노드이다
-2- w가 검은 노드이다, w.left와 w.right가 검은 노드이다.
-3- w가 검은 노드이다, w.left가 빨간 노드면서 w.right가 검은 노드이다.
-4- w가 검은 노드이다, w.right가 빨간 노드이다.

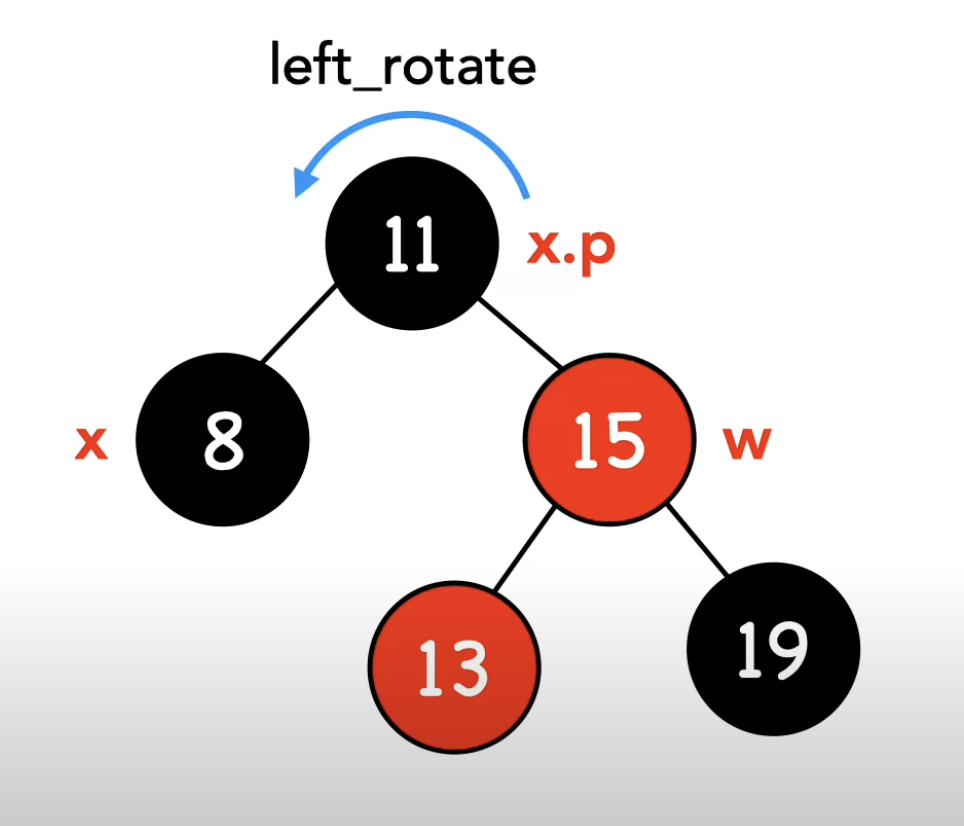
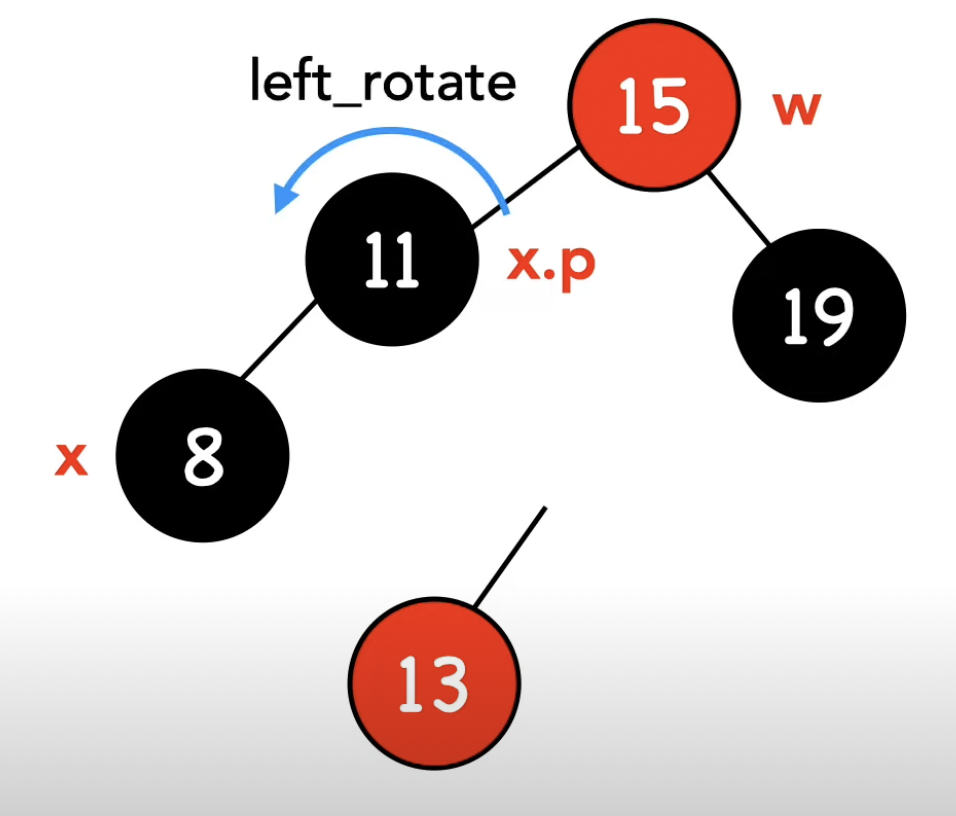
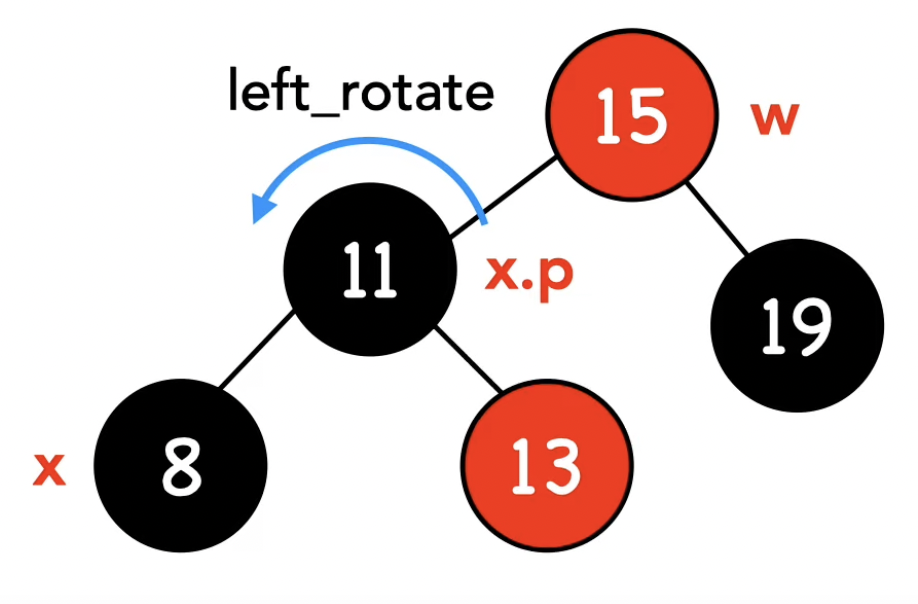
-1- w가 빨간 노드이다
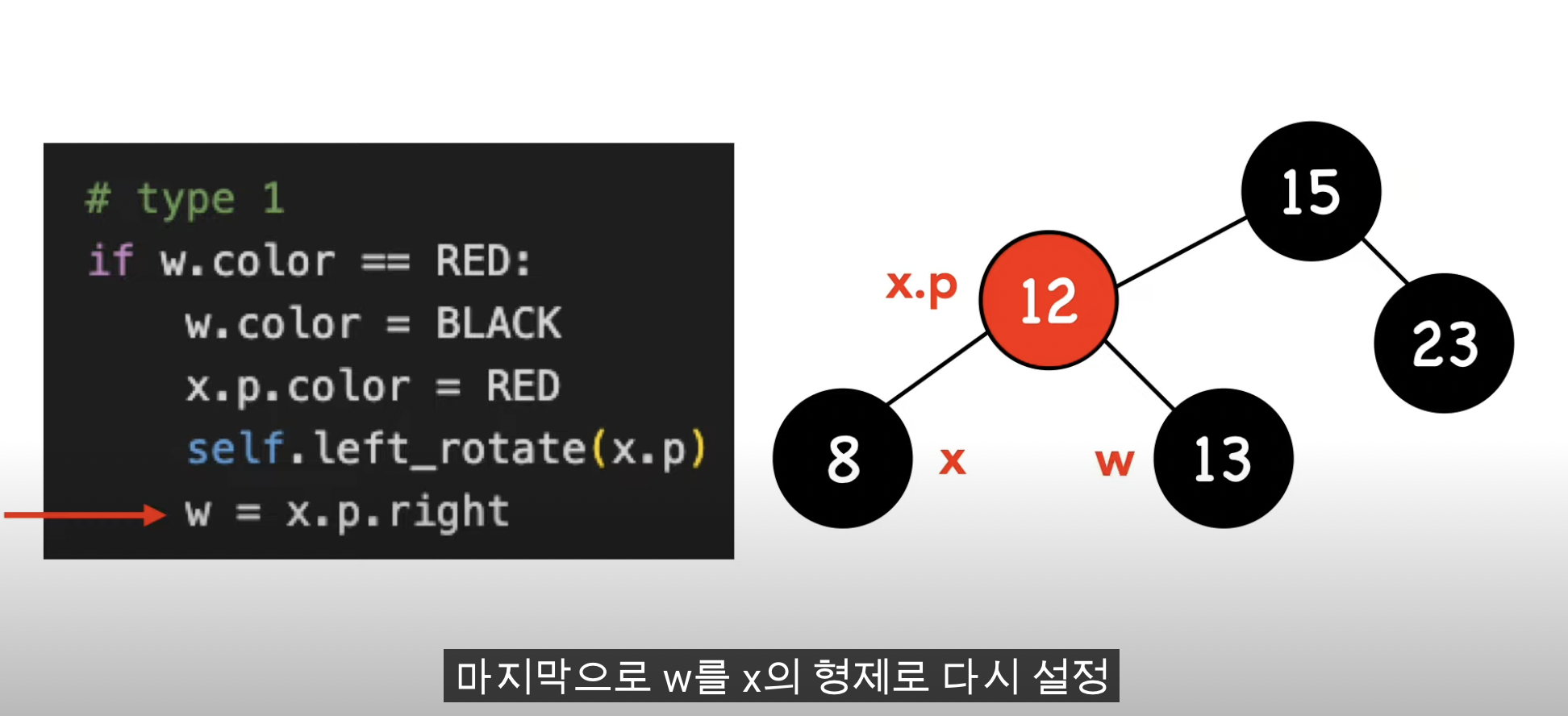
-2- w가 검은 노드이다, w.left와 w.right가 검은 노드이다.


-3- w가 검은 노드이다, w.left가 빨간 노드면서 w.right가 검은 노드이다.
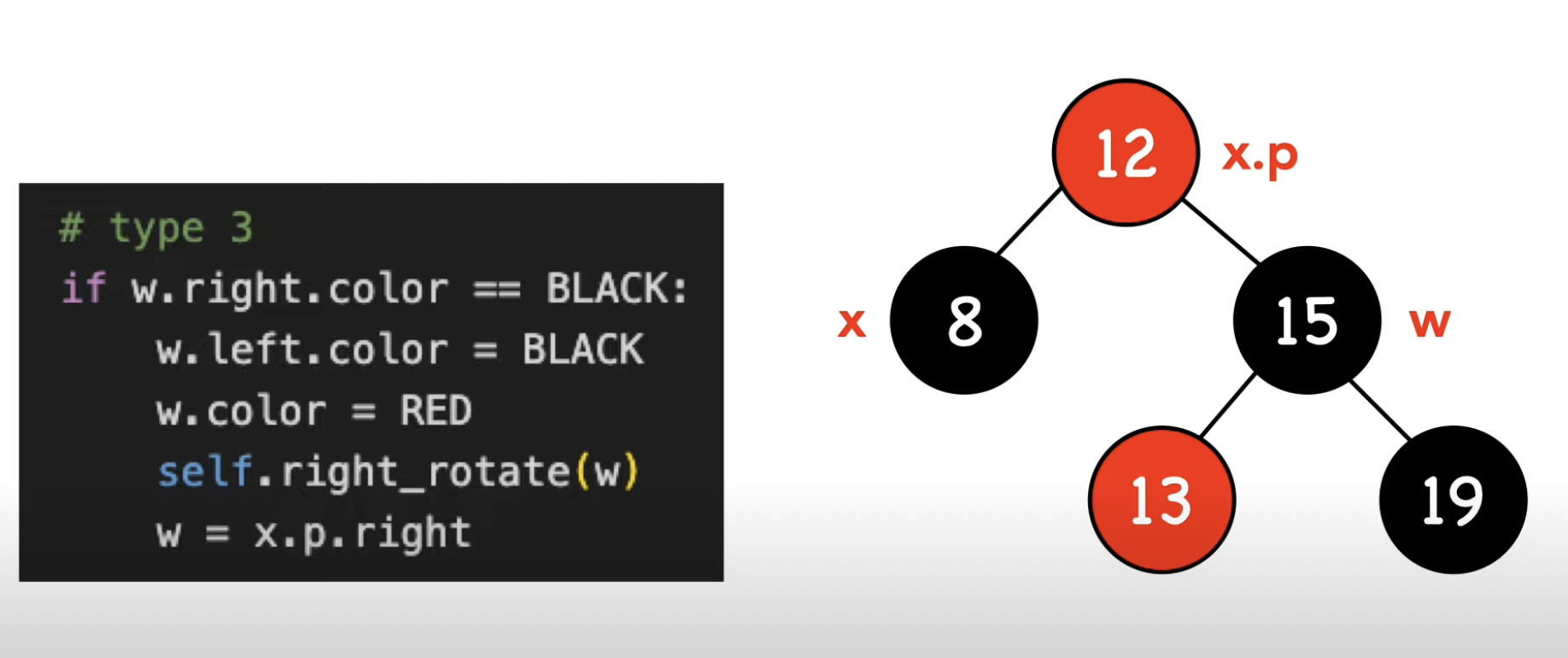
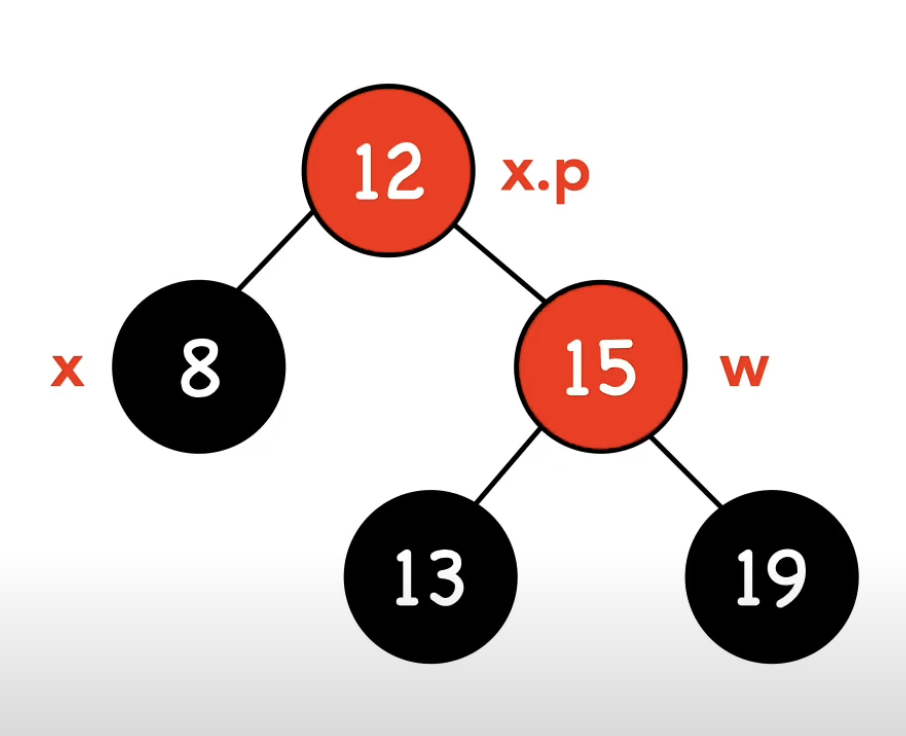
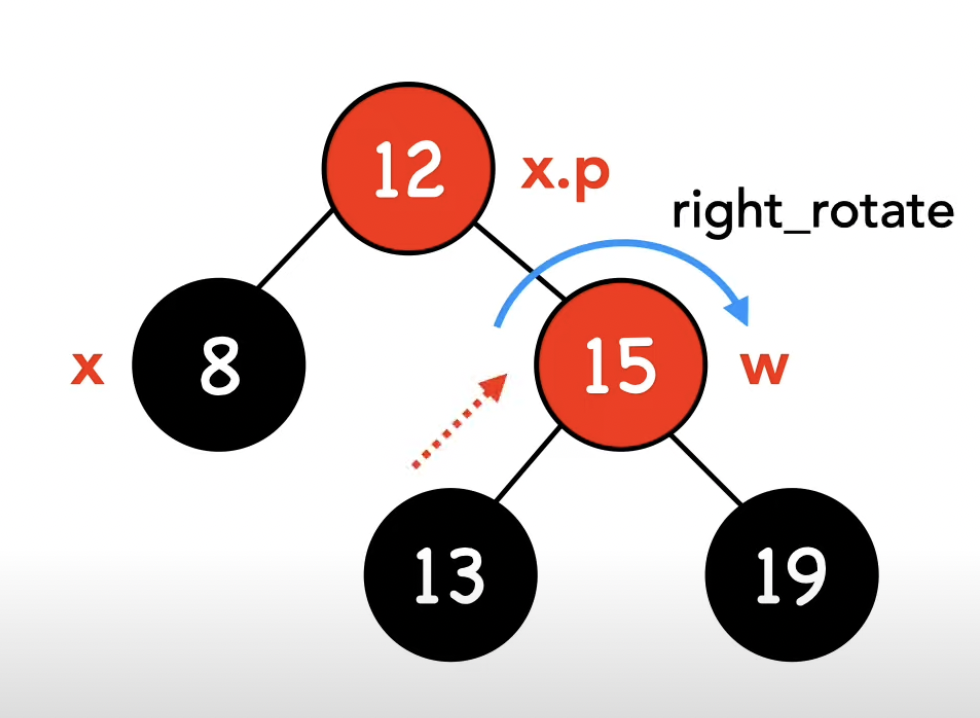
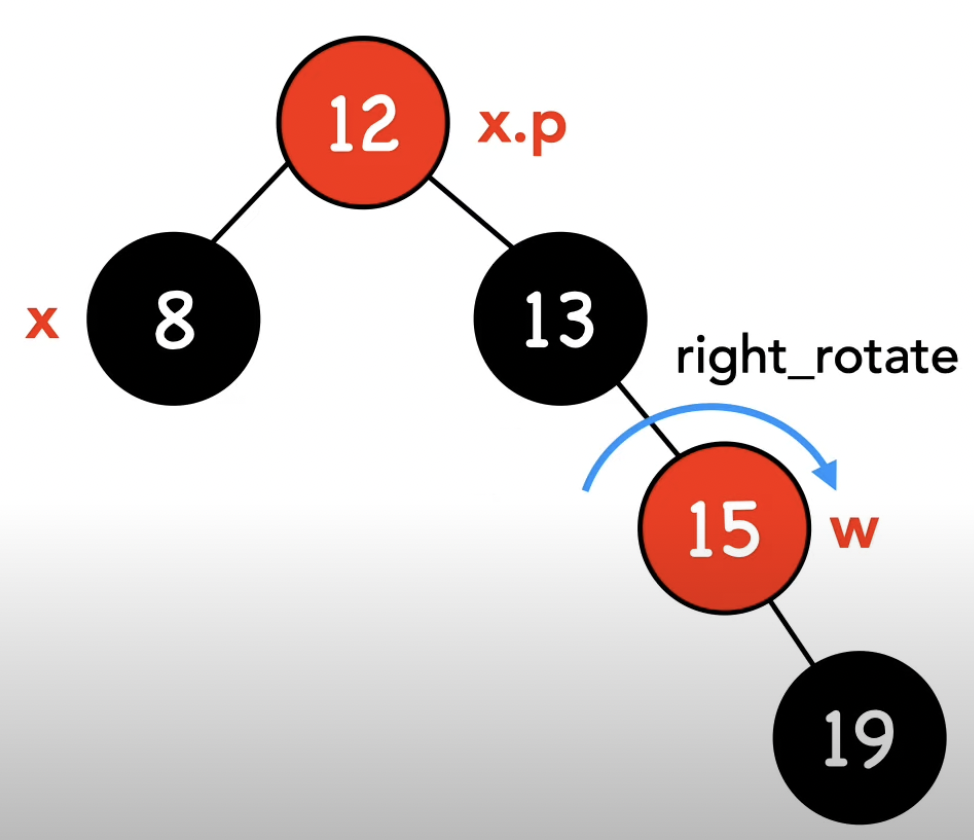
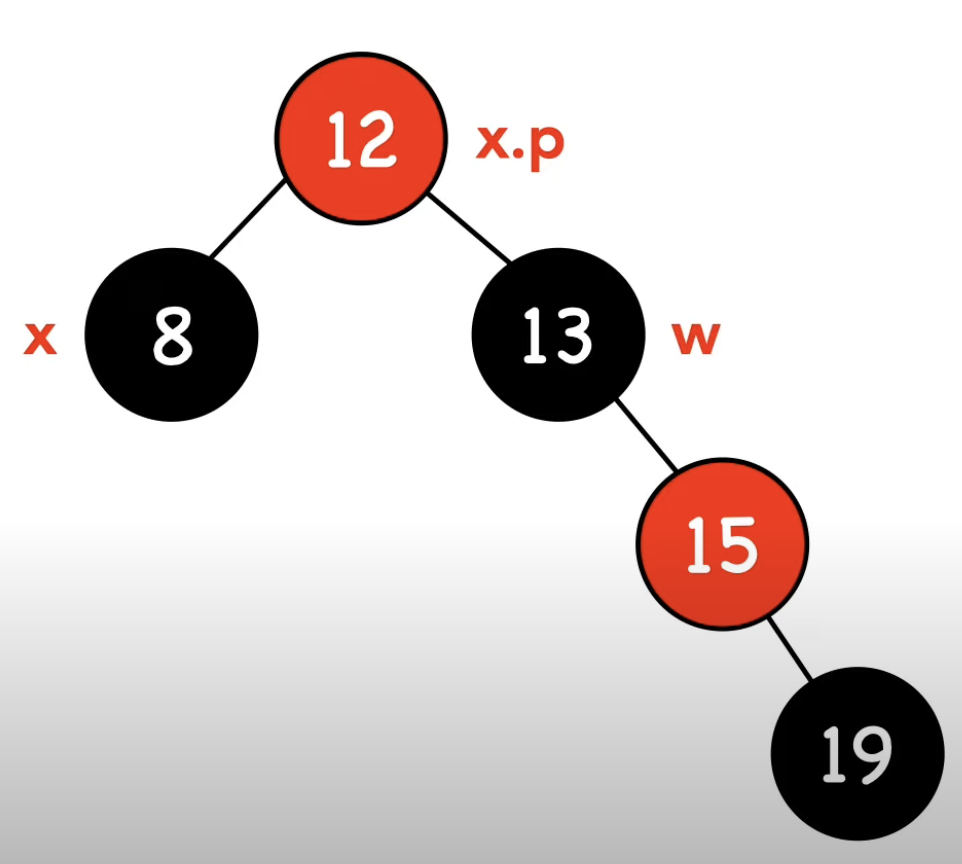
-4- w가 검은 노드이다, w.right가 빨간 노드이다.
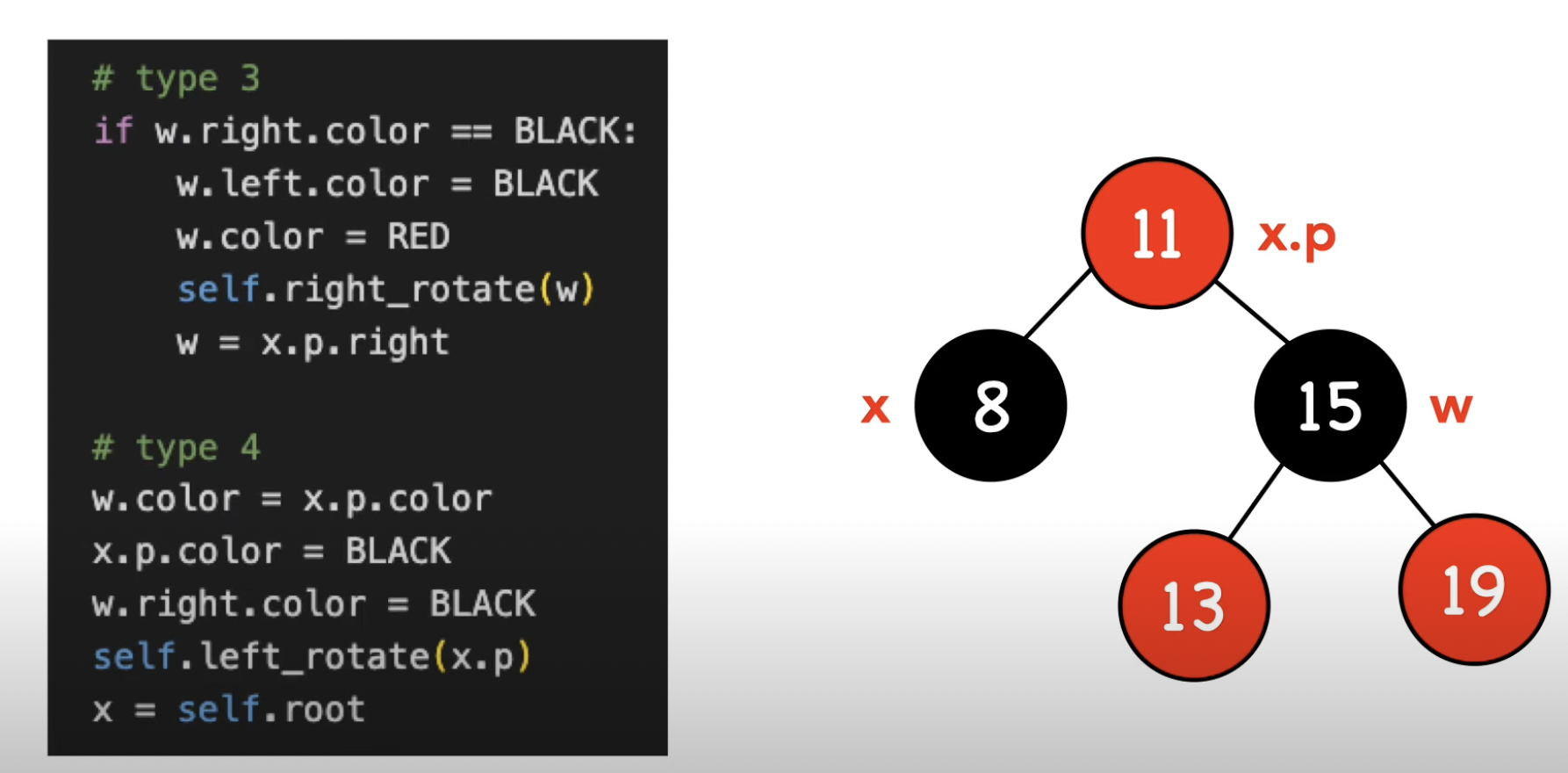
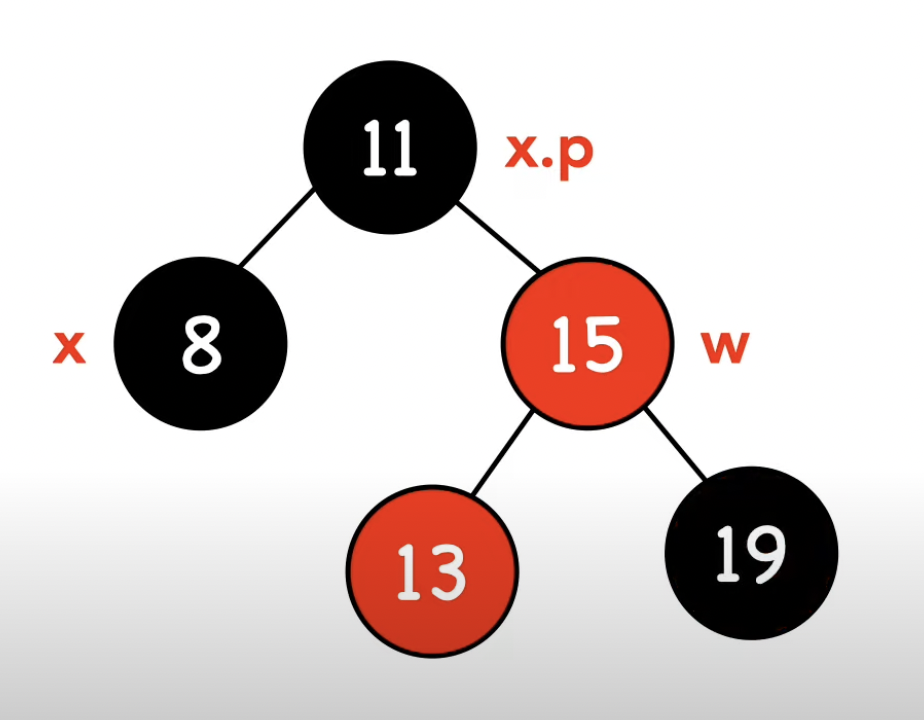

void rbtree_erase_fixup(rbtree *t, node_t *x) {
node_t *w;
while (x != t->root && x->color == RBTREE_BLACK) { // x가 root가 되면 그냥 검은색으로 바꾸면된다. while문 아래는 x가 doubly black일 떄 이뤄진다.
if (x == x->parent->left) { // doubly black인 x가 왼쪽 자식일 때
w = x->parent->right; // 형제 노드 w
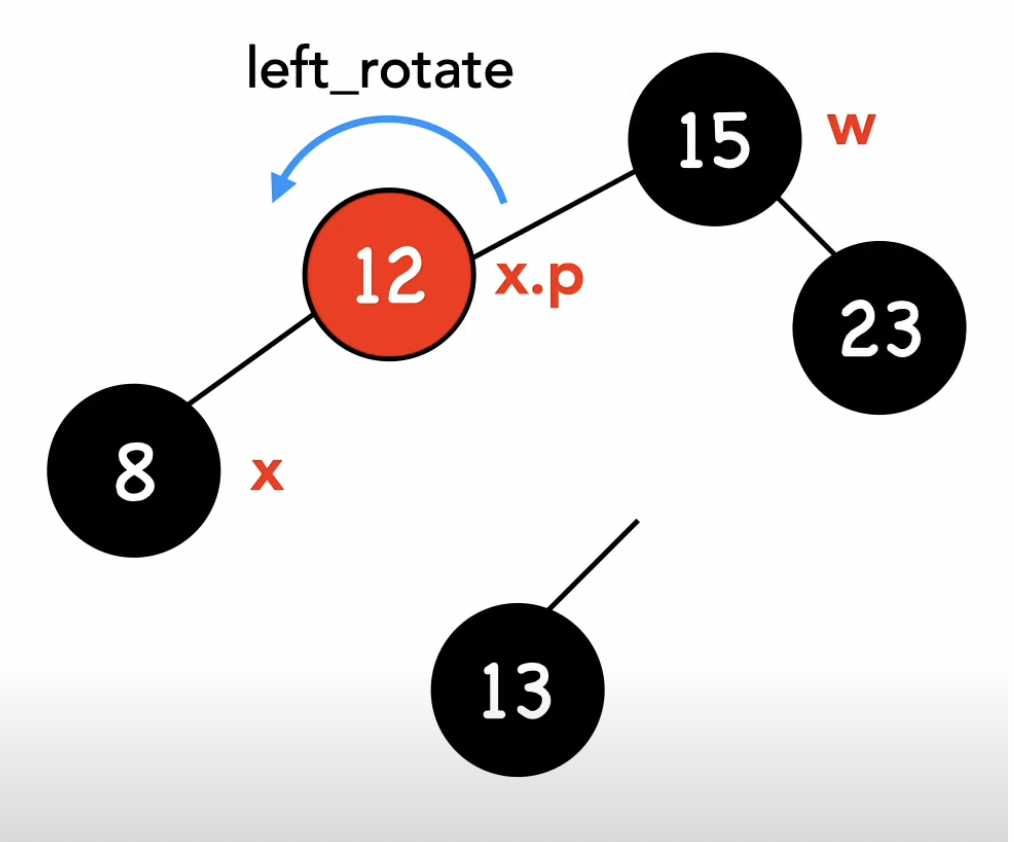
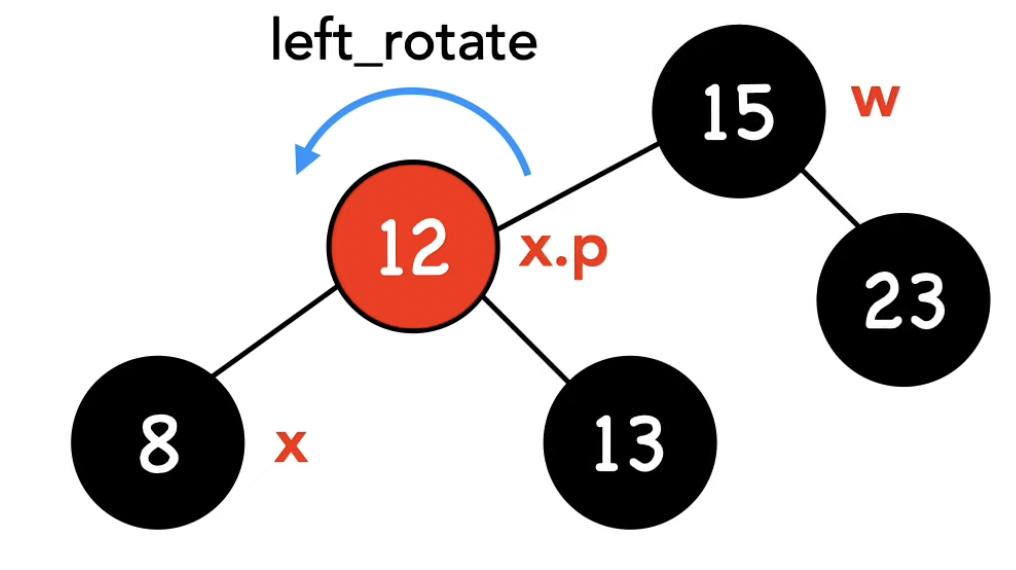
if (w->color == RBTREE_RED) {. // -1- w가 빨간 노드이다 : 부모와 형제의 색을 바꾼 후 부모를 기준으로 왼쪽 회전
w->color = RBTREE_BLACK;
x->parent->color = RBTREE_RED;
left_rotate(t, x->parent);
w = x->parent->right; // 회전을 끝내고 난 후에는 x->parent->right가 새로운 노드 된다. 밑의 if, else if, else(경우 2, 3, 4)의 중 하나로 위임
}
// 위의 if문을 만나지 않았으므로, w->color == RBTREE_BLACK인 경우이다.
// x->parent로 짬 때리는 경우이다.
if (w->left->color == RBTREE_BLACK && w->right->color == RBTREE_BLACK) { // -2- w가 검은 노드이다, w.left와 w.right가 검은 노드이다.
//부모인 형제노드를 red로 칠하고 x를 x의 parent로 선언
w->color = RBTREE_RED;
x = x->parent; // while loop을 통해 위로 올라가면서 탐색한다
} else {
if (w->right->color == RBTREE_BLACK) { // -3- w가 검은 노드이다, w.left가 빨간 노드면서 w.right가 검은 노드이다.
//w 왼쪽 자식과 w의 색상을 바꾼 후 w에 대해 우회전
w->left->color = RBTREE_BLACK;
w->color = RBTREE_RED;
right_rotate(t, w);
w = x->parent->right;
}
w->color = x->parent->color; // -4- w가 검은 노드이다, w.right가 빨간 노드이다.
x->parent->color = RBTREE_BLACK;
w->right->color = RBTREE_BLACK;
left_rotate(t, x->parent);
x = t->root; // 경우 4를 거치면 특성 위반이 해결되는 것이므로 x를 root로 설정하여 while문을 빠져나가도록 한다.
}
//좌우반전 : 지금까지 위에서 ‘rigth’와 ‘left’를 바꾼 경우와 같다
} else {
w = x->parent->left;
if (w->color == RBTREE_RED) { // -1- w가 빨간 노드이다
w->color = RBTREE_BLACK;
x->parent->color = RBTREE_RED;
right_rotate(t, x->parent);
w = x->parent->left;
}
if (w->right->color == RBTREE_BLACK && w->left->color == RBTREE_BLACK) { // -2- w가 검은 노드이다, w.left와 w.right가 검은 노드이다.
w->color = RBTREE_RED;
x = x->parent;
} else {
if (w->left->color == RBTREE_BLACK) { // -3- w가 검은 노드이다, w.left가 빨간 노드면서 w.right가 검은 노드이다.
w->right->color = RBTREE_BLACK;
w->color = RBTREE_RED;
left_rotate(t, w);
w = x->parent->left;
}
w->color = x->parent->color; // -4- w가 검은 노드이다, w.right가 빨간 노드이다.
x->parent->color = RBTREE_BLACK;
w->left->color = RBTREE_BLACK;
right_rotate(t, x->parent);
x = t->root;
}
}
}
x->color = RBTREE_BLACK;
}핵심은 루프와 if문입니다. x가 루트 노드가 아니며, x의 색상이 검은색일 때까지 while 루프를 돌게 됩니다. 이때 x의 색상이 검은색이 아닌 경우는 문제가 없으므로, 검은색일 때의 경우만 처리하면 됩니다.
'Computer Science > 자료구조' 카테고리의 다른 글
| [자료구조, 파이썬] Queue과 Stack의 개념과 구현 (0) | 2023.05.24 |
|---|---|
| [자료구조, 파이썬] Linked list의 특징과 구현, 시간복잡도, 리트코드 문제풀이 (0) | 2023.05.20 |
| [자료구조] Array list와 배열(Array) 개념과 장단점, 시간복잡도 (1) | 2023.05.19 |
| Sentinel node를 사용하여 구현한 레드블랙 트리(1) - 삽입로직 (0) | 2023.04.05 |