| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 파이썬서버
- pandas
- 으
- 정글사관학교
- 미니프로젝트
- 블랙스크린복구
- Express
- R
- nixos한글설정\
- 언리얼뮤지컬
- Bootstrap4
- 스트림릿
- streamlit
- ossca
- Enhanced Input System
- VUE
- 디자드
- 프메
- inxos
- 판다스
- flask
- 오픈소스
- EnhancedInput
- Jinja2
- 마인크래프트뮤지컬
- 알고풀자
- nixos한글키보드
- 메모리인식불량
- 지우개신공 #pc자기진단 #ram미인식 #컴퓨터고장해결 #램인식불량 #pc자가수리 #컴퓨터고장해결 #조립pc
- JWT
- Today
- Total
Today, I will
Sentinel node를 사용하여 구현한 레드블랙 트리(1) - 삽입로직 본문

1. 레드블랙트리 구현해보기
안녕하세요! FlyDuck Dev🦢입니다.
오늘은 레드블랙트리를 구현해보기 위해 삽입 로직을 정리해보고자 합니다. 레드-블랙 트리(Red-Black Tree)는 이진 탐색 트리(Binary Search Tree)의 일종으로, 검색, 삽입, 삭제의 연산에서 최악의 경우에도 시간 복잡도 O(log n)을 보장하는 자료구조입니다. 이를 위해 노드마다 "레드(red)" 또는 "블랙(black)"의 색을 지정하고, 색의 규칙에 따라 노드의 위치와 색을 조정함으로써 트리의 균형을 유지합니다.
레드-블랙 트리의 속성
- 모든 노드는 레드 또는 블랙 중 하나의 색을 갖습니다.
- 루트 노드는 블랙입니다.
- 모든 리프 노드(NIL 또는 NULL)는 블랙입니다.
- 레드 노드의 자식 노드들은 모두 블랙입니다.
- 모든 노드에 대해, 루트 노드부터 해당 노드까지 경로 상에 있는 블랙 노드의 수는 모두 같습니다.
위의 규칙들을 지키면서 삽입, 삭제가 이루어지면, 최악의 경우에도 O(log n)의 시간 복잡도를 보장합니다. 따라서 대용량 데이터의 검색, 삽입, 삭제가 필요한 경우에 사용됩니다.
2. 센티넬 노드가 있는 레드블랙트리
제가 구현해본 것은 센티넬 노드가 있는 레드블랙트리입니다.
Sentinel node를 사용하여 구현한 레드블랙 트리는 일반적인 레드블랙 트리와 크게 다르지 않습니다. 다만 리프 노드를 Sentinel node로 대체하고, 이에 따른 특별한 처리를 추가해주면 됩니다.
구체적으로, Sentinel node는 일반적인 노드와는 다른 색깔(보통 검은색)을 가지고 있어야 합니다.
레드블랙 트리에서 센티넬 노드란 일종의 가상 노드로서, 레드블랙 트리의 모든 리프 노드들이 이 센티넬 노드를 자식으로 갖도록 하는 노드입니다. 센티넬 노드는 일반적인 노드와는 달리, 실제 데이터를 저장하지 않습니다.
센티넬 노드의 역할
- 일반 노드와의 구분
- 센티넬 노드는 실제 데이터를 저장하지 않으므로, 일반 노드와 구분하기 쉽습니다. 따라서 레드블랙 트리의 노드 탐색 과정에서 일반 노드와 센티널 노드를 구분하여 처리할 수 있습니다.
- 트리의 높이 유지
- 레드블랙 트리에서는 노드의 높이를 일정하게 유지해야 합니다. 이를 위해서는 리프 노드의 부모 노드는 항상 블랙 노드이어야 합니다. 하지만 리프 노드가 없을 경우, 부모 노드가 블랙 노드가 아니게 됩니다. 이때 센티넬 노드를 리프 노드 대신 사용함으로써, 트리의 높이를 일정하게 유지할 수 있습니다.
- 삽입 및 삭제 연산의 효율성
- 삽입 및 삭제 연산에서도 센티넬 노드를 활용할 수 있습니다. 노드를 삽입할 때, 일반 노드와 센티넬 노드를 구분하여 처리하면 더 간단한 코드로 구현할 수 있습니다. 또한 노드를 삭제할 때, 삭제한 노드의 자식 노드들을 센티넬 노드에 연결함으로써 노드 삭제 연산의 코드를 간단하게 구현할 수 있습니다.
즉, Sentinel node를 사용하여 구현한 레드블랙 트리에서는 모든 리프 노드가 Sentinel node로 대체됩니다.
이렇게 되면, 삭제할 노드의 자식 노드가 없는 경우에도 Sentinel node를 찾아서 대체할 수 있으므로 삭제 연산이 보다 간단해집니다.
Sentinel node를 사용하여 구현한 레드블랙 트리는 일반적인 레드블랙 트리와 같은 시간 복잡도를 가지고 있으며, 노드 삭제 연산의 처리 시간을 줄일 수 있는 장점을 가지고 있습니다.
3. 삽입로직

(1) rbtree_insert
node_t *rbtree_insert(rbtree *t, const key_t key) {
node_t *y = t->nil; //부모 저장용 parent_node
node_t *x = t->root; //탐색용 child_node
// 새로 삽입할 노드 위치 탐색 : 이진탐색트리 특성 이용하여 key 값 비교하기
while (x != t->nil) { // nil이 아니라면 계속 내려간다.
y = x; // y에는 미리 x의 값(주소값)을 저장해놓는다. parent를 저장해놓기 위해서이다.
if (key < x->key) { // 삽입하려는 값이 현재 x가 가르키는 노드의 키 값보다 작다면 왼쪽으로 탐색한다.
x = x->left;
} else { // 삽입하려는 값이 현재 x가 가르키는 노드의 키 값보다 크다면 오른쪽으로 탐색한다.
x = x->right; // 추가로, 만약 (x->key == key)를 만족하여 중복되는 값이 있다면 else문을 만나 오른쪽에 넣도록 동작하게 된다.
}
}
// while 문을 다 돌게 되면 x는 nil을 가르킴
// 새로운 노드 z 생성(할당)
node_t *z = (node_t *)calloc(1, sizeof(node_t));
z->key = key;
z->parent = y;
if (y == t->nil) { // while문을 1번도 돌지 않았다면 y, 즉 parent는 nil일 것이다.
t->root = z; // while문을 1번도 돌지 않았다는 것은 트리가 비어있다는 뜻, 새로 생성한 노드 z가 rbtree의 root로 된다.
} else if (z->key < y->key) {
y->left = z; // 만약 새로 삽입할 z의 키 값이 parent의 키 값보다 작다면 parent(y)의 왼쪽에 삽입
} else {
y->right = z; // 만약 새로 삽입할 z의 키 값이 parent의 키 값보다 크다면 parent(y)의 오른쪽에 삽입
}
//새로 삽입할 노드 z는 단말 노드(리프 노드, leaf node)이기 때문에 left, right nil
z->left = t->nil;
z->right = t->nil;
z->color = RBTREE_RED;// 새로 삽입할 노드의 색은 red
rbtree_insert_fixup(t, z);// 특성이 위반되는 케이스들 보완
return t->root;
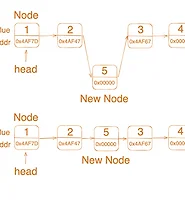
}z의 부모를 y로 설정하는 이유는, 삽입할 위치를 찾아내기 위한 이진 탐색트리의 탐색 과정에서 이미 탐색 경로를 따라 내려가면서 현재 노드를 x라는 변수로 저장해 놓았기 때문입니다. 따라서 새로운 노드 z를 삽입하기 위해 적절한 위치를 찾아내면, z의 부모 노드를 y로 설정하여 바로 이전 단계에서 저장해 놓았던 x를 활용하여 회전 연산 등의 추가 작업을 수행할 수 있습니다.
함수 내부에서는 새로 삽입할 노드의 위치를 찾기 위해 while문을 이용하여 이진탐색트리의 특성을 이용해 탐색을 진행합니다. 탐색 중에는 노드 x와 그의 부모 노드 y를 각각 저장합니다.
while문을 탈출하면, x는 t->nil을 가리키게 됩니다. 이후 새로운 노드 z를 동적으로 할당하고 삽입할 key값을 저장합니다. 이때 삽입할 노드 z의 부모는 바로 이전에 저장해둔 y가 됩니다.
이진탐색트리에서의 위치를 찾은 후, 삽입하려는 노드의 부모를 설정해주고, 노드 z를 단말노드로 만들기 위해 z의 left와 right를 t->nil로 설정합니다. 그리고 새로 삽입한 노드의 색깔을 red로 설정합니다.
그 다음 rbtree_insert_fixup 함수를 호출해 레드블랙트리의 성질을 유지하도록 해줍니다. 이 함수에서는 새로 삽입한 노드 z를 대상으로 하는 다양한 케이스를 처리하여 레드블랙트리의 4가지 성질을 만족시킵니다.
마지막으로 루트 노드를 반환해줍니다.
(2) rbtree_insert_fixup
시뮬레이션 홈페이지 : https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
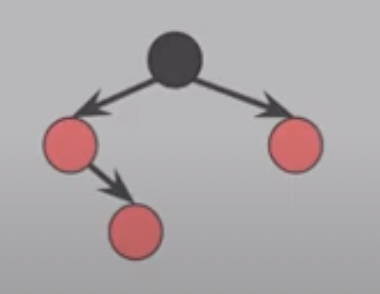
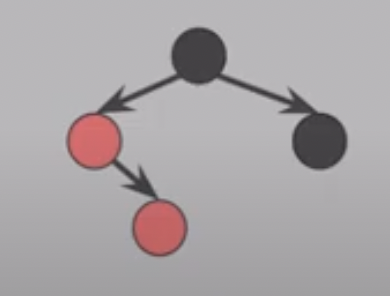
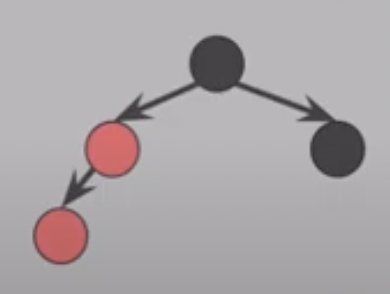
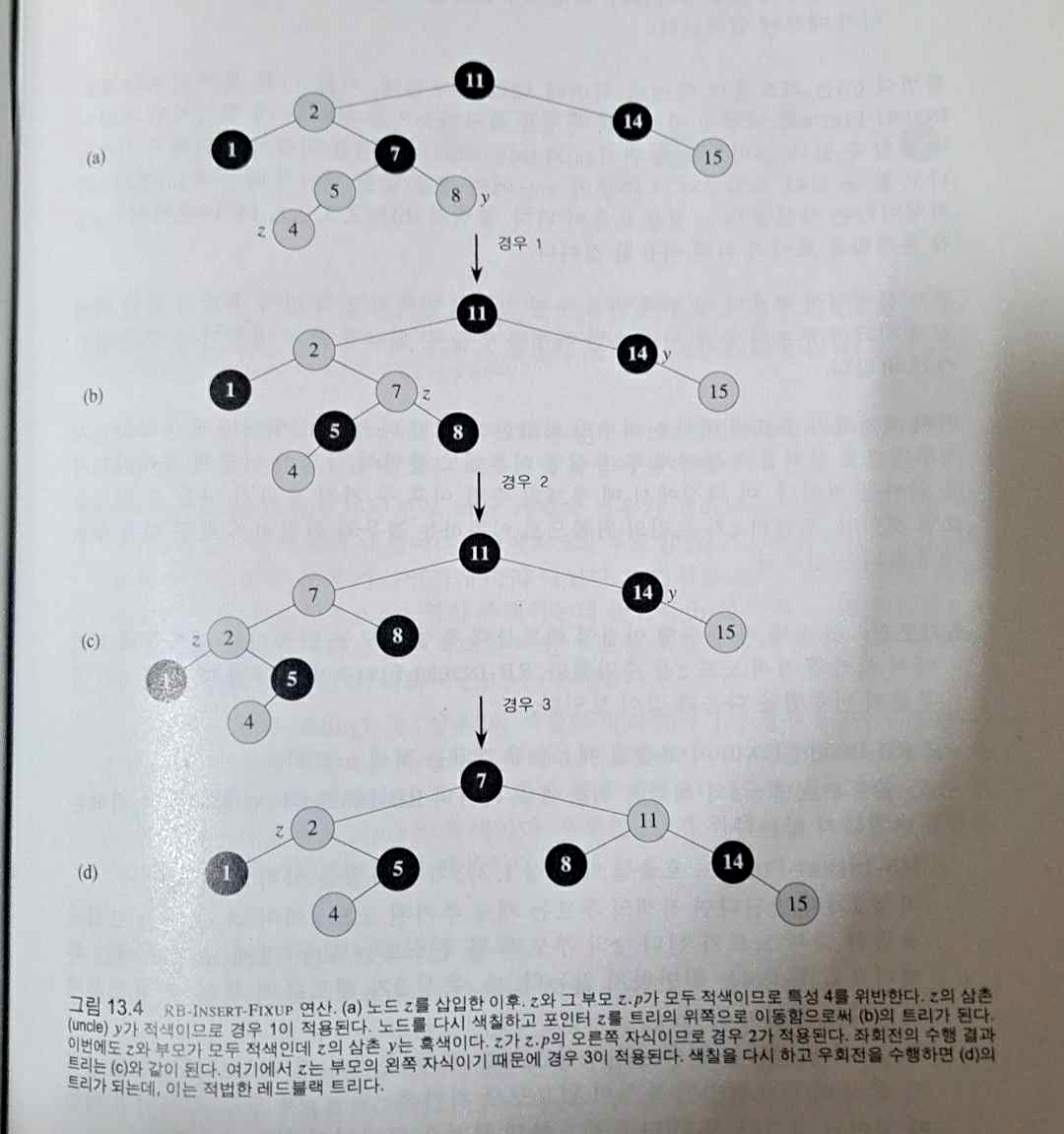
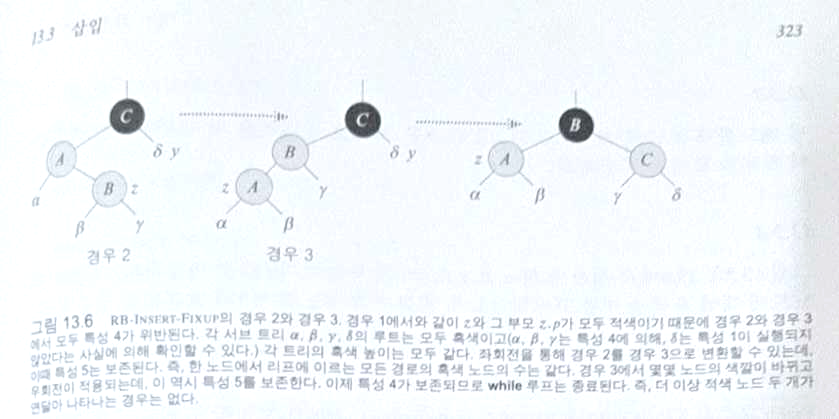
rbtree_insert_fixup 함수는 레드블랙 트리에서 노드를 삽입한 후 발생하는 특성 위반 상황을 처리하여 트리의 균형을 맞추는 역할을 합니다. 이 함수를 통해 새로 삽입한 노드의 색상을 조정하고, 회전 연산을 수행하여 트리를 재조정합니다.

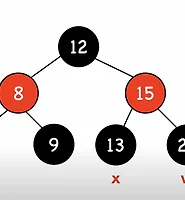
- 경우(1) z의 삼촌 y가 적색인 경우

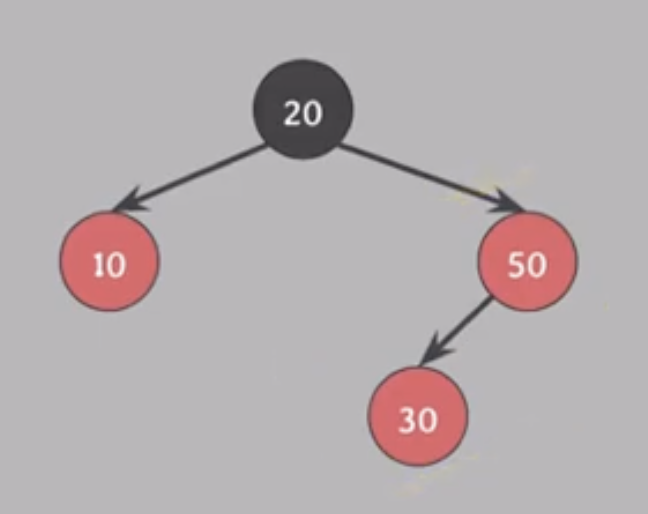
- 경우(2) z의 삼촌 y가 흑색이며 z가 오른쪽 자식인 경우

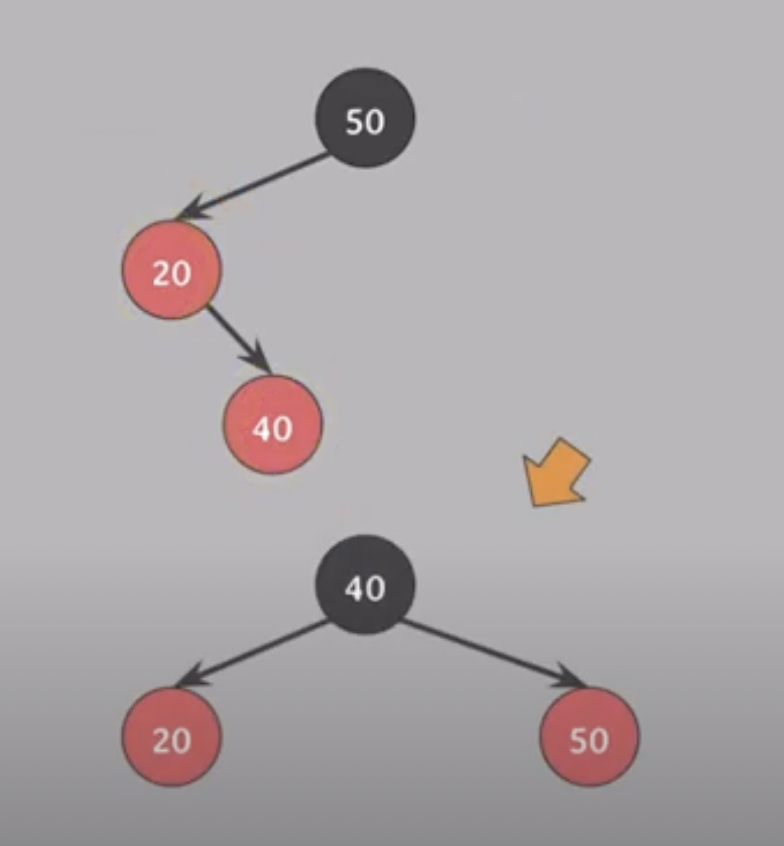
- 경우(3) z의 삼촌 y가 흑색이며 z가 왼쪽 자식인 경우

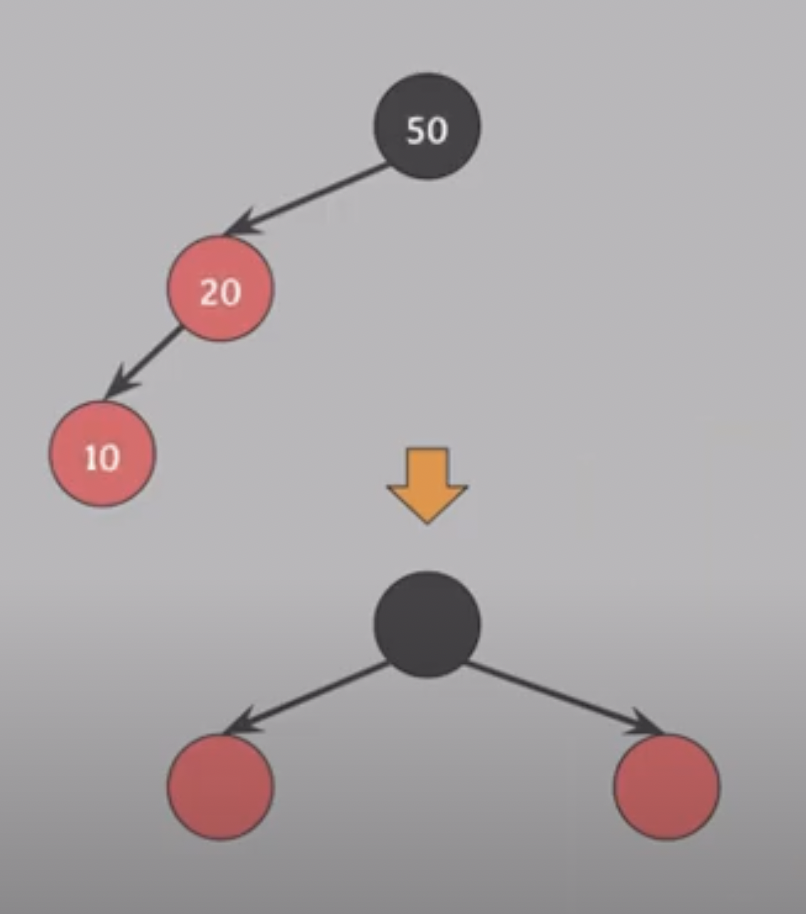
rbtree_insert_fixup 함수는 삽입한 노드 z를 인자로 받습니다.
- 삽입한 노드가 루트 노드인 경우, 노드의 색을 검은색으로 변경합니다.
- 삽입한 노드의 부모 노드가 블랙인 경우, 새로운 노드를 삽입해도 레드블랙 트리의 모든 조건을 만족하므로 추가적인 처리를 하지 않습니다.
- 삽입한 노드의 부모 노드가 레드인 경우, 부모 노드와 삼촌 노드가 모두 레드인 경우와 블랙인 경우로 나누어 처리합니다.
void rbtree_insert_fixup(rbtree *t, node_t *z) {
while (z -> parent -> color == RBTREE_RED) {// 특성 4를 위반한 경우: 레드 노드의 자식 노드들은 모두 블랙
// a. z의 부모가 조부모의 왼쪽 자식이라면
if (z->parent == z-> parent -> parent -> left) {
node_t *uncle = z -> parent -> parent -> right; // z 조부모의 오른쪽 자식이 uncle
// 경우 1에 해당(부모도 red, 삼촌도 red), uncle이 red라면 색깔 조정을 하는 것만으로 특성 4 위반을 보완할 수도 있다.
if (uncle -> color == RBTREE_RED) {
z->parent->color = RBTREE_BLACK; // 부모를 black으로
uncle->color = RBTREE_BLACK; // 삼촌도 black으로
z -> parent -> parent -> color = RBTREE_RED; // 조부모는 red로
z = z -> parent -> parent; // 조부모를 기준으로 재탐색
// 경우 2, 3에 해당, uncle이 black이라면 z, parent, parent의 parent가 linear인지 혹은 triangle인지 따져보고 회전 및 색깔 조정
} else {
// 경우 2. 삽입된 red가 부모의 오른쪽 자녀
// triangle을 linear로 만들어줘야 한다.
if (z == z->parent->right) { // 만약 z가 부모의 오른쪽 자식이었다면, 부모가 grand parent의 왼쪽 자식이었으므로 triangle에 해당한다.
z = z->parent; // z의 부모를 축으로 삼아
left_rotate(t, z); // 부모를 기준으로 왼쪽으로 회전해야 한다.
}
// 경우 3. 삽입된 red가 부모의 왼쪽 자녀
// 바로 위의 if문을 거치고 밑의 코드를 거치게 되면 경우 3에 해당
// linear라면 색깔 조정 후 회전하면 된다.
// 색깔 조정 : 부모(red), 조부모(black) 색상을 각각 black, red로 변경
// right_rotate를 진행
z -> parent -> color = RBTREE_BLACK;
z -> parent -> parent -> color = RBTREE_RED;
right_rotate(t, z->parent->parent);
}
// b. z의 부모노드가 조부모의 오른쪽 자식이라면
} else {
// 삼촌 노드는 조부모의 왼쪽 자식
node_t *uncle = z->parent->parent->left;
// 경우 1에 해당(부모도 red, 삼촌도 red)
if (uncle->color == RBTREE_RED) {
z->parent->color = RBTREE_BLACK;
uncle->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
z = z->parent->parent;
} else { // 삼촌이 black 이라면
// 경우 2. 신규 red가 부모노드의 왼쪽 자식이라면
if (z == z->parent->left) {
z = z->parent;
right_rotate(t, z); // 부모를 기준으로 오른쪽 회전 진행
}
// 경우 3. 신규 red가 부모노드의 오른쪽 자식이라면
z->parent->color = RBTREE_BLACK;
z->parent->parent->color = RBTREE_RED;
left_rotate(t, z->parent->parent);
}
}
}
// 특성 2 적용 : 루트 노드는 블랙
t->root->color = RBTREE_BLACK;
}rbtree_insert_fixup 함수를 통해 레드블랙 트리의 특성을 유지하면서 새로운 노드를 삽입할 수 있습니다.

(3) 회전 로직
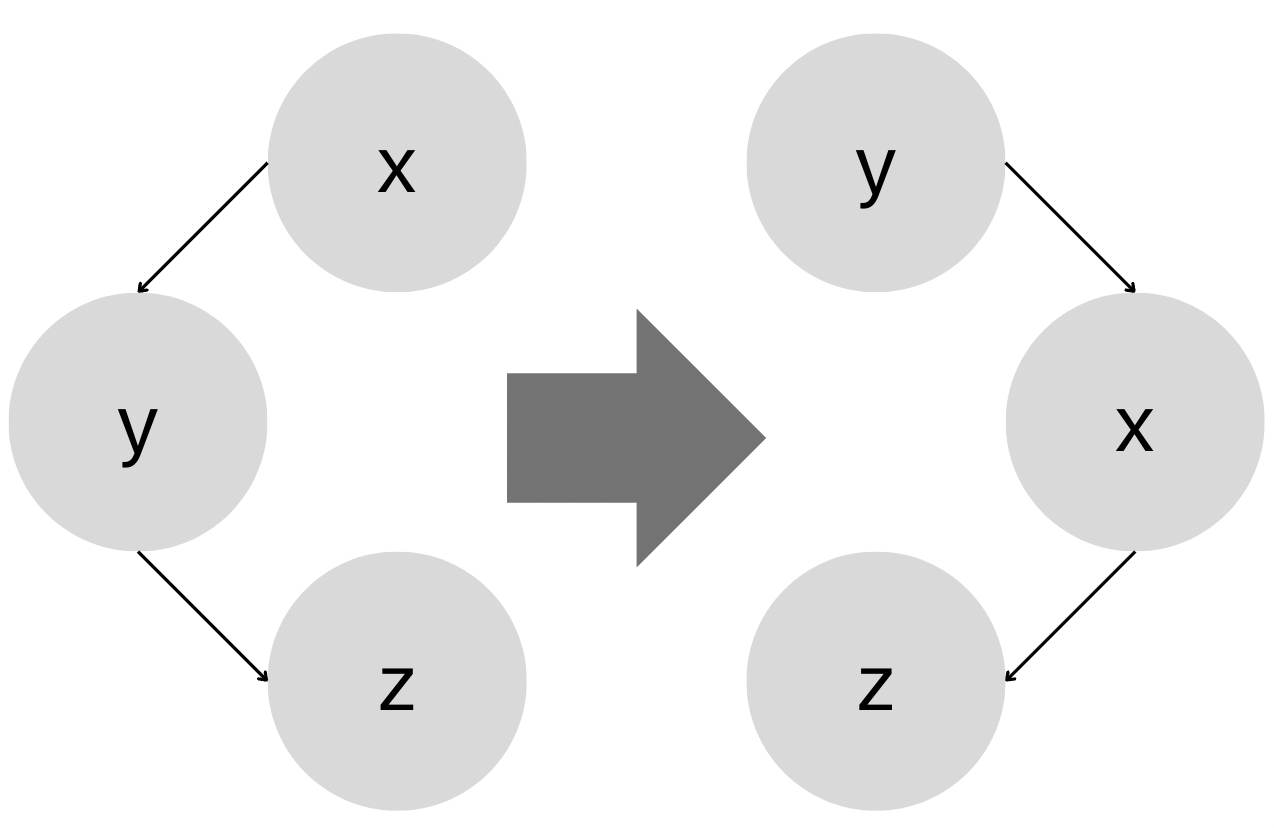
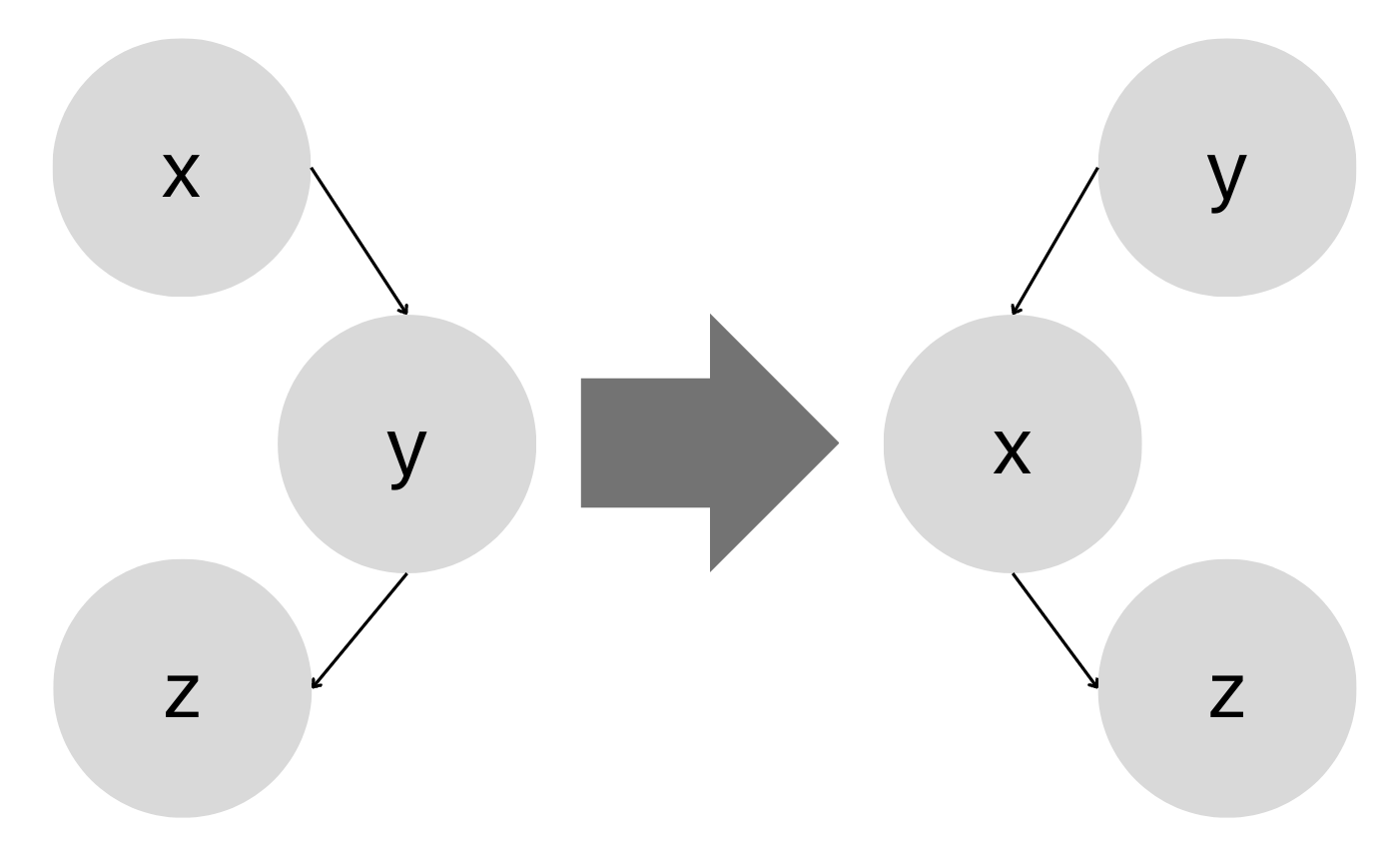
-1- 오른쪽 회전
void right_rotate(rbtree *t, node_t *x) { //x는 우회전을 수행할 노드
node_t *y = x->left; //x의 왼쪽 자식인 y
x->left = y->right; //x의 왼쪽 자식에 y의 오른쪽 자식을 저장
if (y->right != t->nil) { //y의 오른쪽 자식이 t의 빈 노드를 가리키고 있지 않다면,
y->right->parent = x; //그 자식의 부모를 x로 설정
}
y->parent = x->parent; //y의 부모를 x의 부모로 설정
if (x->parent == t->nil) { //x의 부모가 t의 빈 노드라면, y를 t의 루트로 설정
t->root = y;
} else if (x->parent->right == x) { //x가 부모의 오른쪽 자식이라면
x->parent->right = y; //y를 부모의 오른쪽 자식으로 설정
} else { //그 외의 경우에는 y를 부모의 왼쪽 자식으로 설정
x->parent->left = y;
}
y->right = x; //x의 오른쪽 자식으로 y를 설정
x->parent = y; //y의 부모를 x로 설정
}
-2- 왼쪽 회전
void left_rotate(rbtree *t, node_t *x) {
node_t *y = x->right;
x->right = y->left;
if (y->left != t->nil) {
y->left->parent = x;
}
y->parent = x->parent;
if (x->parent == t->nil) {
t->root = y;
} else if (x == x->parent->left) {
x->parent->left = y;
} else {
x->parent->right = y;
}
y->left = x;
x->parent = y;
}
'Computer Science > 자료구조' 카테고리의 다른 글
| [자료구조, 파이썬] Queue과 Stack의 개념과 구현 (0) | 2023.05.24 |
|---|---|
| [자료구조, 파이썬] Linked list의 특징과 구현, 시간복잡도, 리트코드 문제풀이 (0) | 2023.05.20 |
| [자료구조] Array list와 배열(Array) 개념과 장단점, 시간복잡도 (1) | 2023.05.19 |
| Sentinel node를 사용하여 구현한 레드블랙 트리(2) - 삭제로직 (0) | 2023.04.05 |