| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 마인크래프트뮤지컬
- 스트림릿
- JWT
- 파이썬서버
- 정글사관학교
- Bootstrap4
- nixos한글설정\
- 블랙스크린복구
- R
- 디자드
- inxos
- 프메
- 판다스
- flask
- 언리얼뮤지컬
- ossca
- streamlit
- Express
- 오픈소스
- 메모리인식불량
- 으
- Jinja2
- pandas
- 지우개신공 #pc자기진단 #ram미인식 #컴퓨터고장해결 #램인식불량 #pc자가수리 #컴퓨터고장해결 #조립pc
- VUE
- Enhanced Input System
- nixos한글키보드
- 알고풀자
- EnhancedInput
- 미니프로젝트
- Today
- Total
Today, I will
LSE, Least Squares Estimation(최소 제곱 추정) 본문
LSE는 Least Squares Estimation(최소 제곱 추정)의 약자이다. LSE는 주어진 데이터에 가장 잘 맞는 선형 모델을 찾는 방법 중 하나로, 데이터 포인트와 모델의 예측 값 사이의 차이(오차)를 최소화하는 방식으로 동작한다. 여기서 최소화하는 것은 오차의 제곱합이다.
1. SSE (Sum of Squared Errors , 오차 제곱합 )
SSE는 각 데이터 포인트에서 실제 값과 예측 값 사이의 차이를 제곱한 뒤 모두 더한 값이다. SSE를 최소화하는 것이 LSE의 목표이다.

2. 미분을 통해 최적화
w와 b를 구하기 위해, 오차를 최소화하려면 SSE를 미분하고 이를 0으로 만드는 값을 찾아야 한다. 이는 미분이 그래프에서 최소값을 찾는 방법이기 때문이다. 그래서 아래 식에서 보여주듯이, SSE를 각각 w와 b에 대해 미분한 결과가 0이 되도록 하는 값을 찾는다.
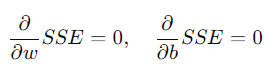
이 과정을 통해 w와 b의 값을 계산할 수 있다.
3. hatw와 hatb 계산
LSE는 실제로 기울기 hatw와 절편 hatb을 다음과 같은 수식으로 구한다:

이 계산 과정을 통해 최적의 선형 모델을 만들 수 있다. 즉, y = wx + b 형태의 직선을 데이터에 가장 잘 맞게 그릴 수 있게 된다.
4. 그래프 설명
아래의 3D 그래프는 SSE 값이 w와 b에 따라 어떻게 변화하는지를 시각화한 것이다. 곡면의 가장 낮은 부분이 SSE를 최소화하는 지점이다. 이 지점에서 w와 b 값을 찾으면, 주어진 데이터에 가장 잘 맞는 선형 모델이 완성된다.

5. LSE 결론
LSE는 주어진 데이터에 가장 잘 맞는 선형 모델을 찾기 위해 오차 제곱합(SSE)을 최소화하는 방법이다. 이 과정에서 기울기 w와 절편b를 계산하고, 이를 통해 데이터에 가장 적합한 직선을 찾는다.
결론적으로, Least Squares Estimation (LSE)수식은 아래와 같이 기울기w와 절편b를 계산하는 공식이다:

즉, LSE의 핵심 수식은 이 두 가지다. 이 수식들을 사용하여 주어진 데이터에 가장 잘 맞는 직선의 기울기와 절편을 구할 수 있다.
6. MSE, SSE 정리
MSE는 오차의 제곱합을 데이터의 개수로 나누어 평균을 내는 방식이다.
SSE(Sum of Squared Errors)를 MSE로 변환할 수 있다.
(1) SSE와 MSE의 차이
- SSE(Sum of Squared Errors): 오차들의 제곱을 모두 더한 값
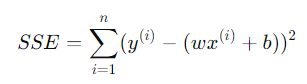
- MSE(Mean Squared Error): SSE를 데이터의 개수 으로 나눈 값. 즉, 평균 제곱 오차
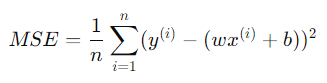
'Computer Science > 인공지능,딥러닝' 카테고리의 다른 글
| [인공지능, 딥러닝] 데이터 클러스터링과 차원 축소 (1) | 2024.10.22 |
|---|---|
| transforms.Normalize의 역할과 중요성 (1) | 2024.10.15 |
| 정규 분포의 확률 밀도 함수(PDF, Probability Density Function) (0) | 2024.10.15 |
| PyTorch와 torchvision으로 MNIST 데이터셋 다루기 (2) | 2024.10.10 |
| sklearn의 load_digits 데이터 분석과 classification 학습 (0) | 2024.10.06 |



