| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 언리얼뮤지컬
- 파이썬서버
- pandas
- 정글사관학교
- VUE
- R
- 알고풀자
- 미니프로젝트
- ossca
- 마인크래프트뮤지컬
- Express
- 프메
- EnhancedInput
- Bootstrap4
- 지우개신공 #pc자기진단 #ram미인식 #컴퓨터고장해결 #램인식불량 #pc자가수리 #컴퓨터고장해결 #조립pc
- inxos
- nixos한글설정\
- nixos한글키보드
- 오픈소스
- 으
- streamlit
- 판다스
- Jinja2
- 스트림릿
- 블랙스크린복구
- 메모리인식불량
- 디자드
- Enhanced Input System
- flask
- JWT
- Today
- Total
Today, I will
[그래픽스] 선형대수-행렬, 그래픽스 프로그래밍에서 자주 쓰는 연산 본문
출처:
LearnOpenGL - Transformations
LearnOpenGL - Transformations
Transformations Getting-started/Transformations We now know how to create objects, color them and/or give them a detailed appearance using textures, but they're still not that interesting since they're all static objects. We could try and make them move by
learnopengl.com
번역:
[Learn OpenGL 번역] 2-7. 시작하기 - 변환(Transformations) (tistory.com)
[Learn OpenGL 번역] 2-7. 시작하기 - 변환(Transformations)
변환(Transformations) 시작하기/변환(Transformations) 우리는 이제 오브젝트를 생성하고 컬러를 입히고 텍스처를 이용하여 세밀하게 표현하는 방법을 알고 있지만 정적인 오브젝트이기 때문에 여전히
heinleinsgame.tistory.com
*Learn Open GL Docs에서 벡터와 행렬 연산에 관하여 핵심 요약한 포스팅입니다.
*한정현 교수님 그래픽스 2장도 추가로 참고하였습니다.
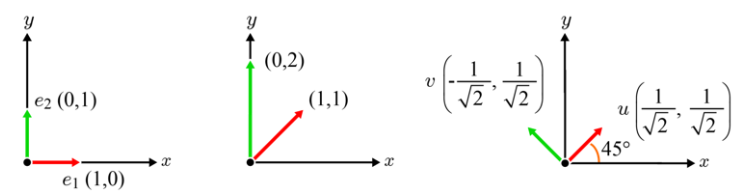
벡터
길이
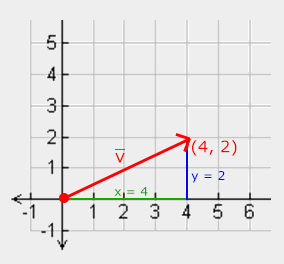
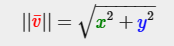
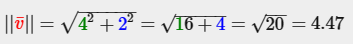
주어진 벡터를 자기 자신의 길이로 나눈 것을 정규화(normalization)이라 하고, 그 길이는 항상 1이기 때문에 단위 벡터라고 부른다.
덧셈과 뺄셈
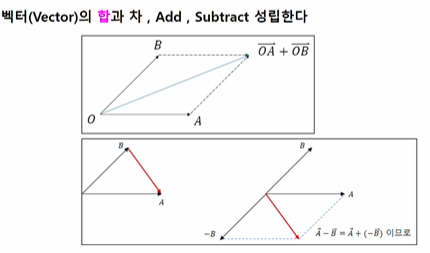
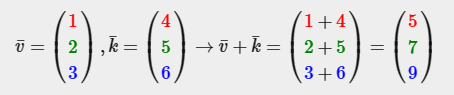
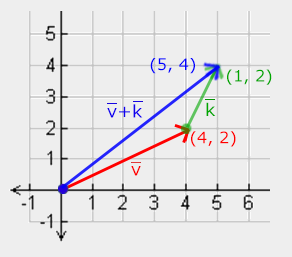
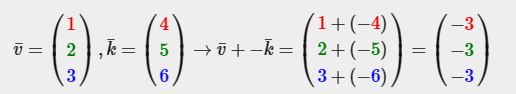
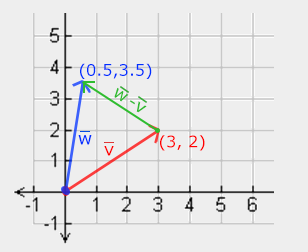
벡터와 벡터의 곱셈
곱셈을 할 때에 선택할 수 있는 2개의 특정한 경우가 있다. 하나는 v¯⋅k¯로 표기 되는 내적(dot product)이고 다른 하나는 v¯×k¯로 표기 되는 외적(cross product)이다.
내적 (Dot Product)
각도가 0도면 코사인은 1을 나타내며 각도가 90도면 코사인은 0을 나타낸다. 내적을 이용하여 두 벡터가 직각(orthogonal)인지 아닌지 혹인 평행한지 아닌지 확인할 수 있다.
단위 벡터가 아닌 두 벡터에 대해서도 각도를 계산할 수 있지만 결과로 나온 값을 두 벡터의 길이로 나누어줘야 cosθ만 남게된다.

내적은 요소들끼리 서로 곱하는 것이다. 두 단위 벡터의 내적은 다음과 같다(두 벡터의 길의는 정확히 1)
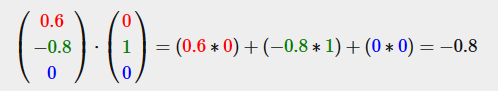
두 벡터 사이의 각도를 계산하기 위해 코사인의 역함수 cos−1를 사용한다. 이 공식을 이용하여 두 벡터 사이의 각도를 효과적으로 계산할 수 있다. 내적은 빛 계산을 할 때 아주 유용하다.
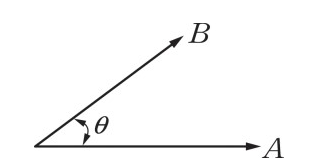
A,B 사이의 각도를 θ 라고 하면 내적 값은
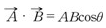
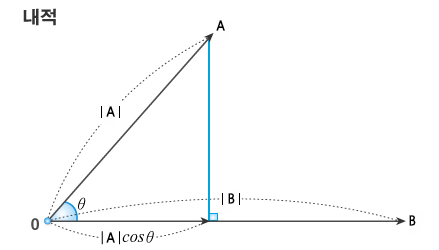
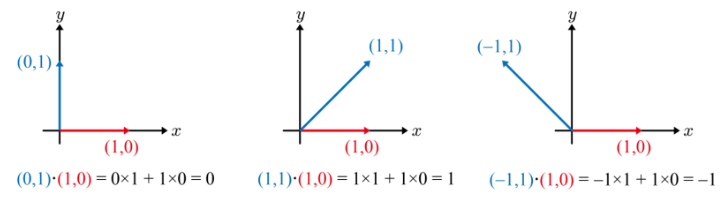
두 벡터 a,b가 수직이라면 a내적b는 0이다. 예각을 형성하면 a내적b는 양수, 둔각이면 a내적b는 음수
단위벡터를 자기자신과 내적하면 1이 된다.
언리얼예시
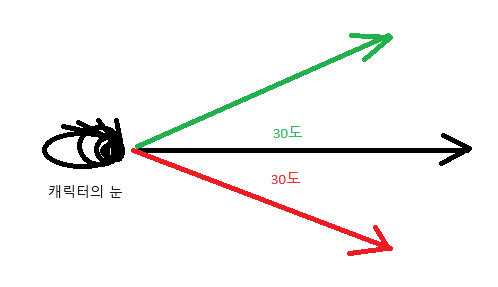
캐릭터가 바라보는 방향을 기준으로 Z축 기준 +-30 각도의 방향 벡터
//회전된 방향 계산
FVector Forward = GetActorForwardVector();
Forward.Normalize();
FVector LeftDirection = Forward.RotateAngleAxis(-30.0f, FVector::UpVector);
FVector RightDirection = Forward.RotateAngleAxis(30.0f, FVector::UpVector);
//두 벡터 사이의 각도
float Dot = FVector::DotProduct(Forward, LeftDirection);
float AcosAngle = FMath::Acos(dot);
float AngleDegree = FMath::RadiansToDegrees(AcosAngle);
// AngleDegree = 30.0f
외적 (Cross Product)
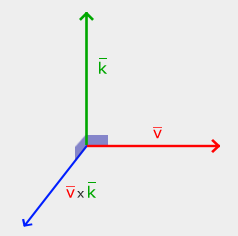
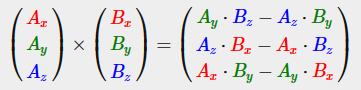
행렬
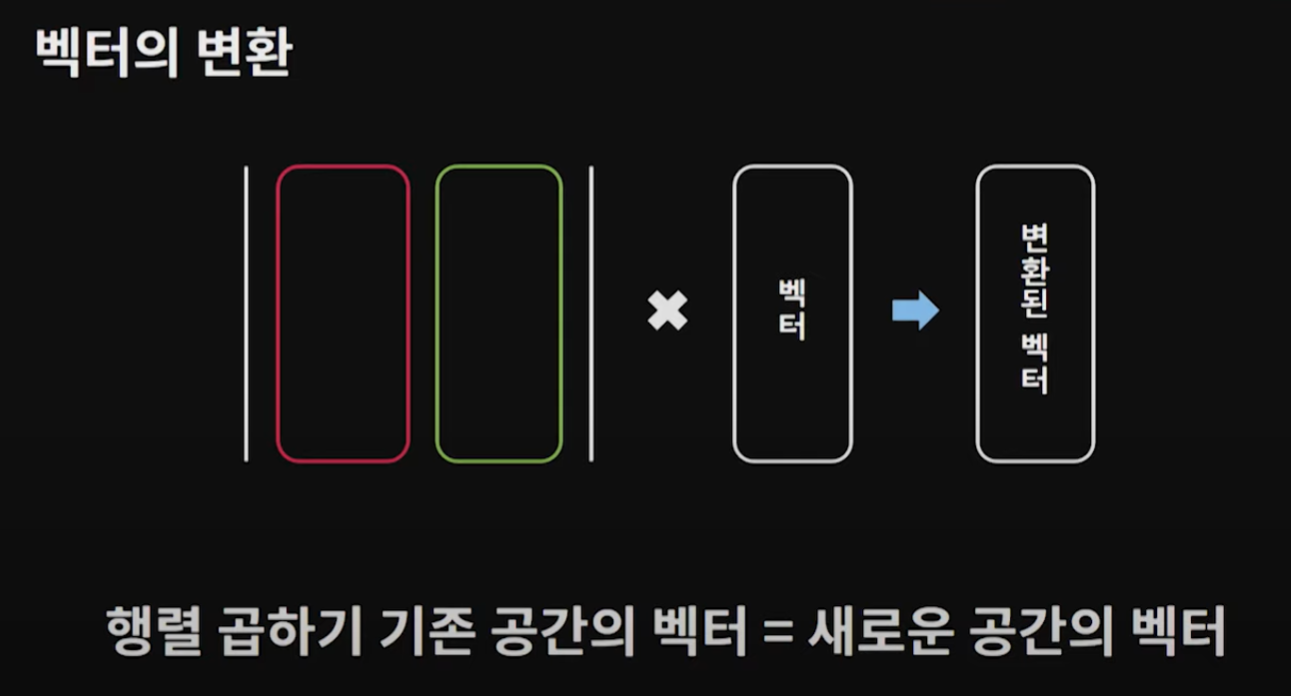
많은 흥미로운 2D/3D 변환들은 행렬 내부에 있고 벡터에 그 행렬을 곱하면 우리의 벡터가 변환(transform)된다.
단위 행렬 I
단위 행렬은 정사각행렬에서 대각선 원소는 1이고 나머지 원소가 모두 0인 경우이다.
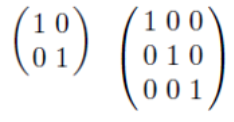
임의의 행렬 M에 대해서 MI = IM = M이라는 공식이 성립한다.
두 개의 정사각행렬이 곱해져서 그 결과가 단위행렬 I라면, 역행렬관계이다.
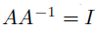
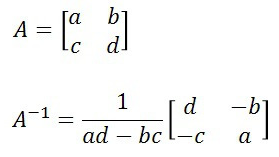
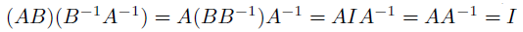
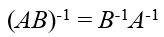
Identity matrix

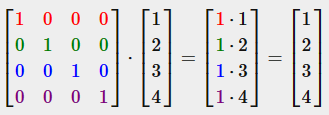
Scaling(확대/축소)
벡터 v¯=(3,2) 를 스케일한다치면, 우리는 x의 축으로 0.5만큼 스케일하여 2배로 줄어들 것이다. 그리고 y축으로 2만큼 스케일하 2배로 길어질 것이다. 벡터를 (0.5, 2)로 스케일하면 아래와 같이 결과는 s¯ 벡터이다.
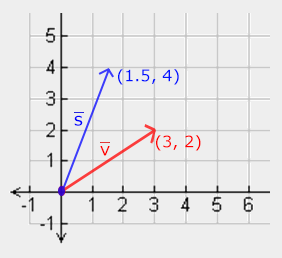
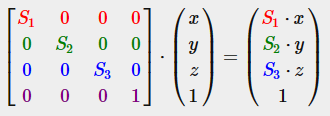
OpenGL은 일반적으로 3D 공간에서 동작한다. 이 2D 예시에서는 z축의 스케일 값을 1로 설정할 수 있다. 그렇게 하면 영향을 끼치지 않는다. 위 스케일 연산은 비균일(non-uniform)스케일이다. 스케일링 요소가 각 축마다 같지 않기 때문입니다. 스칼라가 모든 축에서 동일하다면 균일 스케일(uniform sacle)이라고 부른다.
Translation(이동)
Translation은 원본 벡터 위에 다른 벡터를 더하여 다른 위치의 새로운 벡터를 반환하는 작업이다.
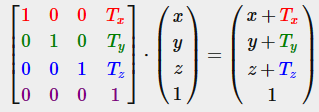
Rotation(회전)
3D에서의 회전은 각도와 회전축으로 지정된다. 지정된 각도는 주어진 회전 축을 따라 개체를 회전시킨다. 머리를 어느 정도 회전시키면서 계속해서 단일 회전축을 내려다보는 것을 시각화하면 쉽다.
삼각법을 사용하면 각도가 주어지면 벡터를 새로 회전된 벡터로 변환할 수 있다. 회전 행렬은 3D 공간에서 각 단위 축에 대해 정의되며, 여기서 각도는 세타 기호로 표시된다 θ
.
X축을 중심으로 회전:

Y축을 중심으로 회전:
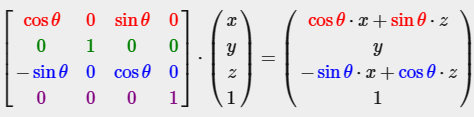
Z축을 중심으로 회전:
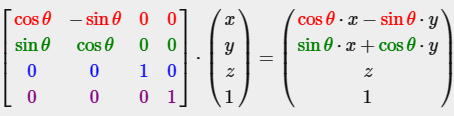
행렬 조합
변환을 위해 행렬을 사용하는 것의 진정한 힘은 여러 변환들을 하나의 행렬에 조합할 수 있다는 것이다.
(x,y,z) 벡터를 가지고 있고 이것을 2만큼 스케일한 후 (1,2,3)만큼 이동시키기 위하여 이동 행렬과 스케일 행렬이 필요하다.
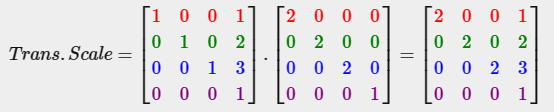
행렬을 곱할 때 먼저 이동을 한 후 스케일 변환을 한다. 행렬 곱은 교환법칙이 성립하지 않기 때문에 순서가 중요하다. 행렬을 곱할 때 가장 오른쪽에 있는 행렬이 벡터와 처음으로 곱해지므로 곱셈은 오른쪽에서 왼쪽으로 읽어야 한다. 행렬을 조합할 때 먼저 스케일 연산을 한 후 회전 연산을 하고 마지막으로 이동 연산을 하는 것을 권장한다. 그렇게 하지 않으면 (부정적인) 효과를 서로에게 줄 수 있다. 예를 들어 먼저 이동을 한 후 스케일링을 했다면 이동 벡터 또한 스케일되어진다.
마지막 변환 행렬을 벡터에 적용하면 결과는 다음 벡터와 같다.
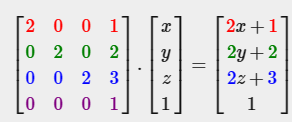
이 벡터는 먼저 2만큼 스케일된 후 (1,2,3)만큼 이동한다.
두 점을 잇는 직선
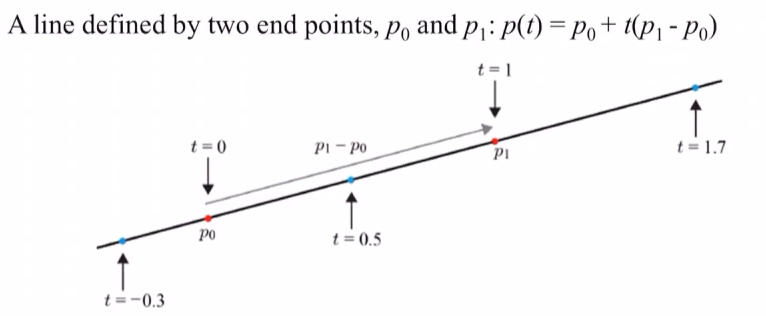
t가 마이너스 무한대에서 무한대까지의 범위를 가진다고 할 때 p(t)로 무한한 직선을 표현 가능하다.
t의 범위가 0에서 무한대까지라면, 한쪽 방향으로만 가게되고 이것을 ray라고 부르게 된다.
선형 보간과 컬러 보간 응

범위를 0부터 1까지로 잡으면 명백하게 선분으로 만들어진다.
p(t) 수식을 풀어서 P0으로 묶으면 선형보간식이 나오게 된다.


컬러 보간으로도 응용이 가능하다.
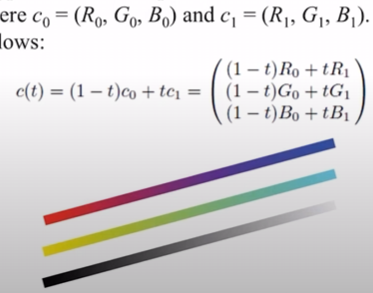
사진의 첫째줄에서 RED는 C0 = (1,0,0), BLUE는 C1=(0,0,1)
중간에서 t는 0.5일 것이므로 Cmid = (0.5, 0, 0.5) 즉 r과 b 요소가 0.5씩 있는 경우에는
마젠타=(1,0,1)이므로 Cmid = 흐린 마젠타가 된다.(사진과 같이)
최종적으로는 빨간색에서 흐린 마젠타를 지나 빨간색이 완전히 희석되어 파란색으로 가는 선분으로 색깔이 지정된다.
(아래 노란색-시안, 흑-백도 같은 원리)
추후 보고싶은 영상: https://youtu.be/nY6cZOY3VOs?feature=shared
'Computer Science > 그래픽스' 카테고리의 다른 글
| [그래픽스] HDR(High Dynamic Range), HDRI (0) | 2024.01.29 |
|---|---|
| [그래픽스] ray tracing intersection with triangle (ray 방정식과 삼각형의 교점 찾기) (1) | 2023.12.15 |
| [그래픽스] 그래픽스 파이프라인 개념과 GPU에서의 쉐이더를 통한 가속화 (0) | 2023.11.17 |
| [OpenGL] opengl graphics pipeline의 이해와 hello_triangle 속 VAO와 VBO의 쓰임 (0) | 2023.10.11 |
| [OpenGL] Learn Open GL 기본 코드 hello_window_clear (1) | 2023.10.10 |




